题目内容
已知某圆心为(1,1),r=3,一条弦AB的中点为(2,3),求弦AB所在直线的方程.
考点:直线与圆的位置关系
专题:计算题,直线与圆
分析:求出kCP=
=2,即可求出以点P(2,3)为中点的弦所在直线方程.
| 3-1 |
| 2-1 |
解答:
解:∵圆心为C(1,1),一条弦AB的中点为P(2,3),则kCP=
=2,
∴以点P(2,3)为中点的弦所在直线方程为y-3=-
(x-2),即x+2y-8=0.
| 3-1 |
| 2-1 |
∴以点P(2,3)为中点的弦所在直线方程为y-3=-
| 1 |
| 2 |
点评:本题考查直线与圆的位置关系,求出kCP=
=2是关键.
| 3-1 |
| 2-1 |

练习册系列答案
相关题目
某检测箱中有10袋食品,其中有8袋符合国家卫生标准,质检员从中任取1袋食品进行检测,则它符合国家卫生标准的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
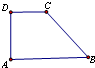 如图,长沙梅溪湖有一块梯形湖面,AB、AD是两条互相垂直的环湖面的公路,CD、CB是两条环湖面的游览小道,且AB=200m,AD=CD=100m.现在A处有一夹角为
如图,长沙梅溪湖有一块梯形湖面,AB、AD是两条互相垂直的环湖面的公路,CD、CB是两条环湖面的游览小道,且AB=200m,AD=CD=100m.现在A处有一夹角为