题目内容
函数 f（x）=lgx+x的零点个数为 个．
考点：根的存在性及根的个数判断
专题：函数的性质及应用
分析：将问题转化为y=lgx与y=-x的交点个数，画出图象，读出即可．
解答：
解：令f（x）=0，得到lgx=-x，
画出y=lgx与y=-x的图象，
如图示：
，
∴函数f（x）有1个零点，
故答案为：1．
画出y=lgx与y=-x的图象，
如图示：
，∴函数f（x）有1个零点，
故答案为：1．
点评：本题考查了函数的零点问题，考查了数形结合思想，是一道基础题．
练习册系列答案
相关题目
曲线x=
y2的焦点的坐标是（ ）
| 1 |
| 3 |
A、(
| ||
B、(0，
| ||
C、(
| ||
D、(0，
|
如图，若圆C：（x+1）2+y2=36上的动点M与点B（1，0）连线的垂直平分线与CM交于点G，则点G的轨迹方程是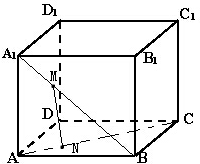
已知正方体ABCD-A1B1C1D1的棱长为a，M、N分别为A1B和AC上的点，A1M=AN=