题目内容
已知函数f（x）=x2+2x+a，
（1）当a=-2时，求不等式f（x）＞1的解集
（2）若对任意的x∈[1，+∞），f（x）＞0恒成立，求实数a的取值范围．
（1）当a=-2时，求不等式f（x）＞1的解集
（2）若对任意的x∈[1，+∞），f（x）＞0恒成立，求实数a的取值范围．
考点：二次函数的性质
专题：函数的性质及应用
分析：（1）当a=-2时，不等式f（x）＞1可化为x2+2x-2＞1，解不等式可得答案；
（2）若对任意的x∈[1，+∞），f（x）＞0恒成立，则a＞-x2-2x在x∈[1，+∞）恒成立，设g（x）=-x2-2x，分析函数在区间[1，+∞）上的单调性，进而可得实数a的取值范围．
（2）若对任意的x∈[1，+∞），f（x）＞0恒成立，则a＞-x2-2x在x∈[1，+∞）恒成立，设g（x）=-x2-2x，分析函数在区间[1，+∞）上的单调性，进而可得实数a的取值范围．
解答：
解：（1）当a=-2时，不等式f（x）＞1可化为x2+2x-2＞1，
即x2+2x-3＞0，
解得{x|x＞1或x＜-3}．
（2）若对任意的x∈[1，+∞），f（x）＞0恒成立，
则a＞-x2-2x在x∈[1，+∞）恒成立，
设g（x）=-x2-2x=-（x+1）2+1
则g（x）在区间[1，+∞）上为减函数
当x=1时g（x）取最小值为-3，
∴a得取值范围为{a|a＞-3}．
即x2+2x-3＞0，
解得{x|x＞1或x＜-3}．
（2）若对任意的x∈[1，+∞），f（x）＞0恒成立，
则a＞-x2-2x在x∈[1，+∞）恒成立，
设g（x）=-x2-2x=-（x+1）2+1
则g（x）在区间[1，+∞）上为减函数
当x=1时g（x）取最小值为-3，
∴a得取值范围为{a|a＞-3}．
点评：本题考查的知识点是二次函数的图象和性质，解二次不等式，恒成立问题，难度不大，属于基础题．
练习册系列答案
寒假天地重庆出版社系列答案
相关题目
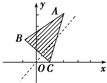在△ABC中，三顶点分别为A（2，4），B（-1，2），C（1，0），点P（x，y）在△ABC内部及其边界上运动，则m=y-x的取值范围为（ ）| A、[1，3] |
| B、[-3，1] |
| C、[-1，3] |
| D、[-3，-1] |