题目内容
在△ABC中,角A、B、C的对边分别为a、b、c,且角A、B都是锐角,a=6,b=5,sinB=
.
(1)求sinA和cosC的值;
(2)设函数f(x)=sin(x+2A),求f(
)的值.
| 1 |
| 2 |
(1)求sinA和cosC的值;
(2)设函数f(x)=sin(x+2A),求f(
| π |
| 2 |
考点:正弦定理,二倍角的余弦
专题:解三角形
分析:(1)由a,b,sinB的值,利用正弦定理求出sinA的值,再由A与B都为锐角,利用同角三角函数间的基本关系求出cosA与cosB的值,根据cosC=-cos(A+B),利用两角和与差的余弦函数公式化简,将各自的值代入计算即可求出值;
(2)将x=
代入f(x)中利用诱导公式及二倍角的余弦函数公式,把cosA的值代入计算即可求出值.
(2)将x=
| π |
| 2 |
解答:
解:(1)∵a=6,b=5,sinB=
,
∴由正弦定理
,得sinA=
=
=
,
∵A、B是锐角,
∴cosA=
=
,cosB=
=
,
∵C=π-(A+B),
∴cosC=cos[π-(A+B)]=-cos(A+B)=-cosAcosB+sinAsinB=-
×
+
×
=
;
(2)由(1)知cosA=
,
∴f(
)=sin(
+2A)=cos2A=2cos2A-1=
-1=
.
| 1 |
| 2 |
∴由正弦定理
| a |
| sinA |
| b |
| sinB |
| asinB |
| b |
6×
| ||
| 5 |
| 3 |
| 5 |
∵A、B是锐角,
∴cosA=
| 1-sin2A |
| 4 |
| 5 |
| 1-sin2B |
| ||
| 2 |
∵C=π-(A+B),
∴cosC=cos[π-(A+B)]=-cos(A+B)=-cosAcosB+sinAsinB=-
| 4 |
| 5 |
| ||
| 2 |
| 3 |
| 5 |
| 1 |
| 2 |
3-4
| ||
| 10 |
(2)由(1)知cosA=
| 4 |
| 5 |
∴f(
| π |
| 2 |
| π |
| 2 |
| 32 |
| 25 |
| 7 |
| 25 |
点评:此题考查了正弦定理,二倍角的正弦函数公式,以及同角三角函数间的基本关系,熟练掌握正弦定理是解本题的关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
若a>b,则下列不等式成立的是( )
| A、lna>lnb | ||||||
| B、0.3a>0.3b | ||||||
C、a
| ||||||
D、
|
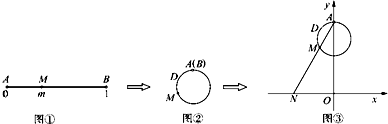 如图展示了一个由区间(0,1)到实数集R的映射过程:区间(0,1)中的实数m对应数轴上的点M,如图①;将线段AB围成一个圆,使两端点A、B恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1),在图形变化过程中,图①中线段AM的长度对应于图③中的弧ADM的长度,如图③.图③中直线AM与x轴交于点N(n,0),则m的象就是n,记作f(m)=n.
如图展示了一个由区间(0,1)到实数集R的映射过程:区间(0,1)中的实数m对应数轴上的点M,如图①;将线段AB围成一个圆,使两端点A、B恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1),在图形变化过程中,图①中线段AM的长度对应于图③中的弧ADM的长度,如图③.图③中直线AM与x轴交于点N(n,0),则m的象就是n,记作f(m)=n.