题目内容
 如图,某几何体中,正三棱柱ABC-A′B′C′的所有棱长都为2,四边形ABCD是菱形,其中P为AC的中点.
如图,某几何体中,正三棱柱ABC-A′B′C′的所有棱长都为2,四边形ABCD是菱形,其中P为AC的中点.(1)求B′P与DC′所成角的大小;
(2)求该几何体的体积.
考点:异面直线及其所成的角,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离,空间角
分析:(1)根据异面直线所成角的定义,作出异面直线B′P与DC′所成的角,再求出它的大小;
(2)该几何体的体积是四棱锥D-AA′C′C的体积与三棱柱ABC-A′B′C′的体积的和.
(2)该几何体的体积是四棱锥D-AA′C′C的体积与三棱柱ABC-A′B′C′的体积的和.
解答:
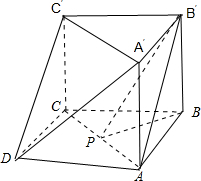 解:(1)连接AB′,PB,如图所示;
解:(1)连接AB′,PB,如图所示;
∵AD∥BC,且AD=BC,
∴AD∥B′C′,且AD=B′C′,
∴四边形ADC′B′是平行四边形,
∴DC′∥AB′,且DC′=AB′;
∴∠AB′P是异面直线B′P与DC′所成的角;
在△AB′P中,
AP=
AC=1,
AB′=
=2
,
B′P=
=
,
∴AP2+B′P2=AB′2;
∴△AB′P是Rt△;
∴cos∠AB′P=
=
=
,
∴∠AB′P=arccos
,
即异面直线B′P与DC′所成的角是arccos
;
(2)该几何体的体积是
V=V四棱锥D-AA′C′C+V三棱柱ABC-A′B′C′
=
×22×
+
×2×
×2=
.
 解:(1)连接AB′,PB,如图所示;
解:(1)连接AB′,PB,如图所示;∵AD∥BC,且AD=BC,
∴AD∥B′C′,且AD=B′C′,
∴四边形ADC′B′是平行四边形,
∴DC′∥AB′,且DC′=AB′;
∴∠AB′P是异面直线B′P与DC′所成的角;
在△AB′P中,
AP=
| 1 |
| 2 |
AB′=
| AB2+BB′2 |
| 2 |
B′P=
| BP2+BB′2 |
| 7 |
∴AP2+B′P2=AB′2;
∴△AB′P是Rt△;
∴cos∠AB′P=
| B′P |
| AB′ |
| ||
2
|
| ||
| 4 |
∴∠AB′P=arccos
| ||
| 4 |
即异面直线B′P与DC′所成的角是arccos
| ||
| 4 |
(2)该几何体的体积是
V=V四棱锥D-AA′C′C+V三棱柱ABC-A′B′C′
=
| 1 |
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
10
| ||
| 3 |
点评:本题考查了空间中的异面直线所成的角的计算问题,也考查了求空间几何体的体积的问题,求空间中的异面直线所成的角,关键是找角,是基础题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
已知全集U=R,集合A={x||x|<3},B={x|x-2≥0},则A∪∁UB等于( )
| A、(-∞,3] |
| B、(-∞,3) |
| C、[2,3) |
| D、(-3,2] |
下列命题中正确的是( )
| A、一直线与一平面平行,这个平面内有无数条直线与它平行 |
| B、平行于同一直线的两个平面平行 |
| C、与两相交平面的交线平行的直线必平行于这两个相交平面 |
| D、两条平行直线中的一条与一个平面平行,则另一条也与该平面平行 |
 如图,四棱锥P-ABCD中,PA⊥平面ABCD,AB∥CD,∠BAD=∠ADC=90°,AB=AD=2CD,E为PB的中点.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,AB∥CD,∠BAD=∠ADC=90°,AB=AD=2CD,E为PB的中点.