��Ŀ����
9�������ĸ�����Բ���ߵ������У�����A��BΪ�������㣬kΪ��������|$\overrightarrow{PA}$|+|$\overrightarrow{PB}$|=k����P�Ĺ켣Ϊ��Բ��
��˫����$\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{9}$=1����Բx2+$\frac{{y}^{2}}{35}$=1����ͬ�Ľ��㣻
�۷���2x2-5x+2=0�������ɷֱ���Ϊ��Բ��˫���ߵ������ʣ�
����֪��FΪ�����������y2=4x�ϵ�����A��B����$\overrightarrow{AF}$=3$\overrightarrow{FB}$������AB���е�P���ߵľ���Ϊ$\frac{8}{3}$��
��������������Ϊ�ۢܣ�
���� �����ⶨ���жϢ٣���Բ���ߵı������жϽ��������������жϢڣ���ⷽ���жϢۣ�����ֱ���������ߵ�λ�ù�ϵ�жϢܣ�
���  �⣺���ڢ٣���k=|AB|ʱ������P�Ĺ켣Ϊ�߶�AB���ʢٴ���
�⣺���ڢ٣���k=|AB|ʱ������P�Ĺ켣Ϊ�߶�AB���ʢٴ���
���ڢڣ�˫����$\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{9}$=1�Ľ�����x���ϣ�����Բx2+$\frac{{y}^{2}}{35}$=1�Ľ�����y���ϣ��ʢڴ���
���ڢۣ���ⷽ��2x2-5x+2=0����${x}_{1}=\frac{1}{2}$��x2=2��
���2x2-5x+2=0�������ɷֱ���Ϊ��Բ��˫���ߵ������ʣ��ʢ���ȷ��
���ڢܣ���ͼ����BF=m���������ߵĶ���֪��AA1=3m��BB1=m��
���ABC�У�AC=2m��AB=4m��${k}_{AB}=\sqrt{3}$��ֱ��AB����Ϊy=$\sqrt{3}$��x-1����
�������߷���������y��3x2-10x+3=0��
AB�е㵽�߾���Ϊ$\frac{{x}_{1}+{x}_{2}}{2}+1=\frac{5}{3}+1=\frac{8}{3}$���ʢ���ȷ��
�ʴ�Ϊ���ۢܣ�
���� ���⿼�����������ж���Ӧ�ã�������Բ���ߵĶ��塢���̼������ʣ����е��⣮

��ϰ��ϵ�д�
�����Ŀ
19��������վ��һ�����࣬��ס�������֮��ǡ��վ���˵ĸ���Ϊ��������
| A�� | $\frac{1}{6}$ | B�� | $\frac{1}{5}$ | C�� | $\frac{1}{3}$ | D�� | $\frac{1}{2}$ |
20���Ӽ���A={-2��-1��2}�����ѡȡһ������Ϊa���Ӽ���B={-1��1��3}�����ѡȡһ������Ϊb����ֱ��ax-y+b=0�������������ĸ���Ϊ��������
| A�� | $\frac{2}{9}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{4}{9}$ | D�� | $\frac{1}{4}$ |
4��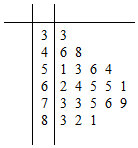 ij��˾�����û������Ʒ����ȵ��ʾ����飬�����ȡ��20���û������֣��õ�ͼ3��ʾ��Ҷͼ���Բ�����75�����֣���Ϊ�û��Բ�Ʒ���⣬������Ϊ�����⣬
ij��˾�����û������Ʒ����ȵ��ʾ����飬�����ȡ��20���û������֣��õ�ͼ3��ʾ��Ҷͼ���Բ�����75�����֣���Ϊ�û��Բ�Ʒ���⣬������Ϊ�����⣬
����������������������2��2�����������ݴ��������K2=3.7781�����ڷ����ĸ��ʲ�����5%��ǰ���£����Ƿ���Ϊ����������롰�Ա��йأ�
����
���� �����û��Ըù�˾�IJ�Ʒ�����⡱�ĸ��ʣ�
���� �ù�˾Ϊ�Կͻ�����һ���ĵ��飬�����������Ʒ������û��������ѡȡ2�ˣ��������˶������û�����Ů�û��ĸ��ʣ�
 ij��˾�����û������Ʒ����ȵ��ʾ����飬�����ȡ��20���û������֣��õ�ͼ3��ʾ��Ҷͼ���Բ�����75�����֣���Ϊ�û��Բ�Ʒ���⣬������Ϊ�����⣬
ij��˾�����û������Ʒ����ȵ��ʾ����飬�����ȡ��20���û������֣��õ�ͼ3��ʾ��Ҷͼ���Բ�����75�����֣���Ϊ�û��Բ�Ʒ���⣬������Ϊ�����⣬����������������������2��2�����������ݴ��������K2=3.7781�����ڷ����ĸ��ʲ�����5%��ǰ���£����Ƿ���Ϊ����������롰�Ա��йأ�
| ������ | ���� | �ϼ� | |
| �� | 4 | 7 | |
| Ů | |||
| �ϼ� |
| P��K2��k�� | 0.100 | 0.050 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
���� �ù�˾Ϊ�Կͻ�����һ���ĵ��飬�����������Ʒ������û��������ѡȡ2�ˣ��������˶������û�����Ů�û��ĸ��ʣ�
14����֪ʵ��x��y����$\left\{\begin{array}{l}x-y+1��0\\ x-3y-1��0\\ x��1\end{array}\right.$����z=kx-y����СֵΪ-5����ʵ��k��ֵΪ��������
| A�� | -3 | B�� | 3��-5 | C�� | -3��-5 | D�� | ��3 |