题目内容
某一物体在某种介质中作直线运动,已知t时刻,它的速度为v,位移为s,且它在该介质中所受到的阻力F与速度v的平方成正比,比例系数为k,若已知s=
t2,则该物体由位移s=0移动到位移s=a时克服阻力所作的功为 .(注:变力F做功W=∫
F(s)ds,结果用k,a表示)
| 1 |
| 2 |
s2 s1 |
考点:定积分的简单应用
专题:导数的综合应用
分析:将变力F用s表示出来,根据变力F做功的公式进行计算即可得到结论.
解答:
解:∵在该介质中所受到的阻力F与速度v的平方成正比,比例系数为k,
∴F=kv2,
∵t时刻,它的速度为v,位移为s,
∴s=
t2,
s′(t)=t,即v=s′(t)=t,
∴s=
t2=
v2,
即v2=2s,
即F=kv2=2ks,
则由W=∫
F(s)ds得W=∫
2ksds=ks2|
=ka2,
故答案为:ka2
∴F=kv2,
∵t时刻,它的速度为v,位移为s,
∴s=
| 1 |
| 2 |
s′(t)=t,即v=s′(t)=t,
∴s=
| 1 |
| 2 |
| 1 |
| 2 |
即v2=2s,
即F=kv2=2ks,
则由W=∫
s2 s1 |
a 0 |
a 0 |
故答案为:ka2
点评:本题主要考查积分的物理意义,要求熟练掌握积分的公式.

练习册系列答案
相关题目
已知点A(-3,1,-4),B(3,-5,10)则线段AB的中点M的坐标为( )
| A、(0,-4,6) |
| B、(0,-2,3) |
| C、(0,2,3) |
| D、(0,-2,6) |
已知圆的方程是(x-2)2+(y-3)2=4,则点P(-3,-2)满足( )
| A、是圆心 | B、在圆上 |
| C、在圆内 | D、在圆外 |
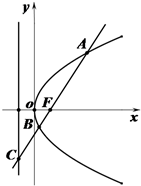 如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=6,则此抛物线的方程为
如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=6,则此抛物线的方程为