题目内容
已知{an}是等差数列,a1=
,a4=
,设bn=sinan•sinan+1•sinan+2,则数列{bn}的通项公式bn= .
| π |
| 6 |
| 7π |
| 6 |
考点:三角函数中的恒等变换应用,等差数列的通项公式
专题:三角函数的图像与性质
分析:首先,根据a1=
,a4=
,求出该等差数列的公差,然后,写出通项公式,再结合三角函数积化和差公式进行求解.
| π |
| 6 |
| 7π |
| 6 |
解答:
解:设等差数列{an}的公差为d,
则a4=a1+3d=
+3d=
,
∴d=
,
∴通项公式an=
(2n-1),
∴an+1=
(2n+1),an+2=
(2n+3),
∵bn=sinan•sinan+1•sinan+2,
∴bn=sinan•sinan+2•sinan+1
=-
[cos(an+an+2)-cos(an-an+2)]•sinan+1
=-
[cos(2an+1)+
]•sinan+1
=-
sinan+1cos2an+1-
sinan+1
=-
×
(sin3an+1-sinan+1)-
sinan+1
=-
sin3an+1+
sinan+1-
sinan+1
=-
sin[3×
(2n+1)]
=-
sin(nπ+
)
=(-1)n-1•
故答案为:(-1)n-1•
.
则a4=a1+3d=
| π |
| 6 |
| 7π |
| 6 |
∴d=
| π |
| 3 |
∴通项公式an=
| π |
| 6 |
∴an+1=
| π |
| 6 |
| π |
| 6 |
∵bn=sinan•sinan+1•sinan+2,
∴bn=sinan•sinan+2•sinan+1
=-
| 1 |
| 2 |
=-
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 1 |
| 2 |
| 1 |
| 4 |
=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
=-
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
=-
| 1 |
| 4 |
| π |
| 6 |
=-
| 1 |
| 4 |
| π |
| 2 |
=(-1)n-1•
| 1 |
| 4 |
故答案为:(-1)n-1•
| 1 |
| 4 |
点评:本题综合考查了等差数列的概念和通项公式,两角和与差的三角函数等知识,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=
(a为非零常数),则f(x)的图象满足( )
| (x-1)2+a |
| x-1 |
| A、关于点(1,0)对称 |
| B、关于点(1,1)对称 |
| C、关于原点对称 |
| D、关于直线x=1轴对称 |
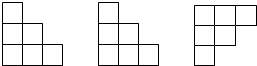 已知若干个正方体小木块堆放在一起形成的组合体的三视图如图所示,则所需小木块最少有多少个( )
已知若干个正方体小木块堆放在一起形成的组合体的三视图如图所示,则所需小木块最少有多少个( )| A、7个 | B、8个 | C、9个 | D、10个 |