Question

在正方体ABCD-A₁B₁C₁D₁中，M是线段A₁C₁上的动点，则异面直线BM与AB₁所成的角的取值范围是（　　）

• A、[

  π

  3

  ，

  π

  2

  )
• B、[

  π

  3

  ，

  π

  2

  ]
• C、(

  π

  6

  ，

  π

  2

  )
• D、(

  π

  6

  ，

  π

  3

  ]

Answer 1

考点：异面直线及其所成的角

专题：计算题,空间角

分析：设正方体的边长为1，A₁M=x（0≤x≤

2

），以A为坐标原点，AB，AD，AA₁所在直线为x，y，z轴建立空间直角坐标系，求出A（0，0，0），B（1，0，0），B₁（1，0，1），M（

2

2

x，

2

2

x，1），再由向量的夹角公式，计算即可得到．

解答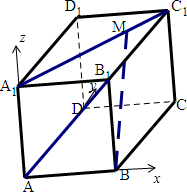： 解：设正方体的边长为1，A₁M=x（0≤x≤

2

），以A为坐标原点，
AB，AD，AA₁所在直线为x，y，z轴建立空间直角坐标系，
则A（0，0，0），B（1，0，0），B₁（1，0，1），M（

2

2

x，

2

2

x，1），
即有

AB1

=（1，0，1），

BM

=（

2

2

x-1，

2

2

x，1），
则cos＜

AB1

，

BM

＞=

AB1 • BM

| AB1 |•| BM |

=

2 2 x-1+1

2 • x2- 2 x+2

=

1

2

•

1

2( 1 x - 2 4 )2+ 3 4

，
由于0≤x≤

2

，则

1

x

≥

1

2

，
则0＜cos＜

AB1

，

BM

＞≤

1

2

，
由于0＜＜

AB1

，

BM

＞≤

π

2

，
则

π

3

≤＜

AB1

，

BM

＞≤

π

2

，
故选B．

点评：本题考查空间异面直线所成的角的求法，考查运用坐标法借助向量的夹角解决的方法，考查运算能力，属于中档题．