题目内容
3.sin10°cos20°cos40°=( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{16}$ |
分析 根据题意,将原式变形可得:原式=$\frac{sin10°cos10°cos20°cos40°}{cos10°}$,运用正弦的二倍角公式进行变形可得原式=$\frac{1}{8}$×$\frac{2sin80°}{cos10°}$,由诱导公式变形可得答案.
解答 解:根据题意,原式=sin10°cos20°cos40°=$\frac{sin10°cos10°cos20°cos40°}{cos10°}$
=$\frac{1}{2}$×$\frac{2sin10°cos10°cos20°cos40°}{cos10°}$=$\frac{1}{4}$×$\frac{2sin20°cos20°cos40°}{cos10°}$
=$\frac{1}{8}$×$\frac{2sin40°cos40°}{cos10°}$
=$\frac{1}{8}$×$\frac{2sin80°}{cos10°}$
=$\frac{1}{8}$×$\frac{sin80°}{sin80°}$=$\frac{1}{8}$;
故选:B.
点评 本题考查二倍角公式的运用,关键是牢记并灵活运用二倍角公式.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
14.过双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F作倾斜角为45°的直线l与双曲线右支交于A、B两点,当a≤|AB|≤4a时,双曲线C的离心率的取值范围为( )
| A. | [$\frac{\sqrt{30}}{5}$,$\frac{\sqrt{6}}{2}$] | B. | (1,$\frac{\sqrt{6}}{2}$] | C. | (1,$\frac{\sqrt{30}}{5}$] | D. | [$\sqrt{2}$,+∞) |
8.在平行六面体ABCD-A′B′C′D′中,模与向量$\overrightarrow{A′B′}$的模相等的向量(不含$\overrightarrow{A′B′}$)有( )
| A. | 3个 | B. | 5个 | C. | 6个 | D. | 7个 |
12.已知实数λ≠0,非零向量$\overrightarrow{a}$及零向量$\overrightarrow{0}$,下列各式不正确的是( )
| A. | $\overrightarrow{0}$•$\overrightarrow{a}$=$\overrightarrow{0}$ | B. | $\overrightarrow{a}$•$\overrightarrow{a}$=$\overrightarrow{a}$2 | C. | $\overrightarrow{a}$-$\overrightarrow{a}$=$\overrightarrow{0}$ | D. | $\overrightarrow{a}$$+\overrightarrow{a}$=2$\overrightarrow{a}$ |
 如图,过曲线C:y=x3(x≥0)上点A1(2,8)作C的切线交x轴于点B1,过点B1作x轴的垂线交曲线C与点A2,过点A2作C的切线交x轴于点B2,再过点B2作x轴的垂线交曲线C与点A3,过点A3作C的切线交x轴于点B3,…、以此类推,得到一系列点:A1,B1,A2,B2,A3,B3,…记点An的横坐标为an.
如图,过曲线C:y=x3(x≥0)上点A1(2,8)作C的切线交x轴于点B1,过点B1作x轴的垂线交曲线C与点A2,过点A2作C的切线交x轴于点B2,再过点B2作x轴的垂线交曲线C与点A3,过点A3作C的切线交x轴于点B3,…、以此类推,得到一系列点:A1,B1,A2,B2,A3,B3,…记点An的横坐标为an.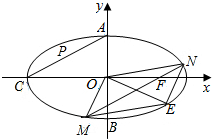 如图:椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0)的上顶点为A,下顶点为B,左顶点为C,F为右焦点,过F作与AC平行的直线交椭圆于M、N两点.
如图:椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0)的上顶点为A,下顶点为B,左顶点为C,F为右焦点,过F作与AC平行的直线交椭圆于M、N两点.