题目内容
15.给出下列命题:①将空间中所有的单位向量移到同一个起点,则它们的终点构成一个圆;
②若空间向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,则$\overrightarrow{a}$=$\overrightarrow{b}$;
③若空间向量$\overrightarrow{m}$,$\overrightarrow{n}$,$\overrightarrow{p}$满足$\overrightarrow{m}$=$\overrightarrow{n}$,$\overrightarrow{n}$=$\overrightarrow{p}$,则$\overrightarrow{m}$=$\overrightarrow{p}$;
④空间中任意两个单位向量必相等;
⑤零向量没有方向;
其中假命题的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据空间向量,向量相等,零向量等向量的基本概念,逐一分析5个结论的真假,可得答案.
解答 解:①将空间中所有的单位向量移到同一个起点,则它们的终点构成一个球,故错误;
②若空间向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,但两个向量的方向是否一致不确定,故$\overrightarrow{a}$=$\overrightarrow{b}$不一定成立,故错误;
③若空间向量$\overrightarrow{m}$,$\overrightarrow{n}$,$\overrightarrow{p}$满足$\overrightarrow{m}$=$\overrightarrow{n}$,$\overrightarrow{n}$=$\overrightarrow{p}$,则$\overrightarrow{m}$=$\overrightarrow{p}$,正确;
④空间中任意两个单位向量模必相等,但方向是否一致不确定,故错误;
⑤零向量方向不确定,但不是没有方向,故错误;
综上可得,综合的命题有4个,
故选:D.
点评 本题以命题的真假判断与应用为载体,考查了空间向量的基本概念,难度不大,属于中档题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
6.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点为F(-c,0),斜率为$\frac{a}{b}$且经过点F的直线l与y2=4cx交于点P,且|OP|=|OF|,O为原点,则双曲线的离心率为( )
| A. | $\frac{1+\sqrt{5}}{2}$ | B. | $\frac{1+\sqrt{3}}{2}$ | C. | $\frac{4\sqrt{2}-2}{7}$ | D. | $\frac{4\sqrt{2}+2}{7}$ |
3.sin10°cos20°cos40°=( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{16}$ |
10.若函数y=f(x)的值域为[$\frac{1}{2}$,3],则函数F(x)=f(x-1)+$\frac{1}{f(x-1)}$的值域是( )
| A. | [$\frac{1}{2}$,3] | B. | [2,$\frac{10}{3}$] | C. | [$\frac{5}{2}$,$\frac{10}{3}$] | D. | [3,$\frac{10}{3}$] |
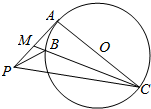 如右图所示,PA为圆O的切线,切点为A,AC是直径,M为PA的中点,MC与圆交于点B.
如右图所示,PA为圆O的切线,切点为A,AC是直径,M为PA的中点,MC与圆交于点B.