题目内容
8．在平行六面体ABCD-A′B′C′D′中，模与向量$\overrightarrow{A′B′}$的模相等的向量（不含$\overrightarrow{A′B′}$）有（ ）| A． | 3个 | B． | 5个 | C． | 6个 | D． | 7个 |
分析 根据平行四边形的对边平行且相等，结合向量与模的定义，写出符合条件的向量即可．
解答 
解：如图所示，平行六面体ABCD-A′B′C′D′中，
模与向量$\overrightarrow{A′B′}$的模相等的向量（不含$\overrightarrow{A′B′}$）有
$\overrightarrow{B′A′}$，$\overrightarrow{AB}$，$\overrightarrow{BA}$，$\overrightarrow{CD}$，$\overrightarrow{DC}$，$\overrightarrow{D′C′}$和$\overrightarrow{C′D′}$共7个．
故选：D．
点评 本题考查了向量与模长的应用问题，是基础题目．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
如图，若P为平行四边形ABCD所在平面外一点，点H为PC上的点，且$\frac{PH}{HC}$=$\frac{1}{2}$，点G在AH上，且$\frac{AG}{AH}$=m，若G，B，P，D四点共面，求m的值．
3．sin10°cos20°cos40°=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{8}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{16}$ |
13．桌面上放着3个半径为1的球，两两相切，在它们上方的空间里放入一个球使其顶点（最高处）恰好和3个球的顶点在同一个平面上，该球的半径为（ ）
| A． | $\frac{\sqrt{2}-1}{2}$ | B． | $\frac{\sqrt{3}-1}{3}$ | C． | $\frac{1}{3}$ | D． | $\frac{\sqrt{3}-1}{2}$ |
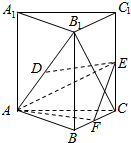已知三棱柱ABC-A1B1C1中，CC1⊥底面ABC，AB=AC，D，E，F分别为B1A，C1C，BC的中点．