题目内容
化简:
+
= .其中θ∈(
,π).
|
|
| π |
| 2 |
考点:三角函数的化简求值
专题:三角函数的求值
分析:利用三角函数的平方关系可将原式化简为
,再由θ∈(
,π)即可求得最简结果.
| (1-cosθ)+(1+cosθ) |
| |sinθ| |
| π |
| 2 |
解答:
解:因为θ∈(
,π),
所以|sinθ|=sinθ,
所以原式=
+
=
=
.
故答案为:
.
| π |
| 2 |
所以|sinθ|=sinθ,
所以原式=
|
|
| (1-cosθ)+(1+cosθ) |
| |sinθ| |
| 2 |
| sinθ |
故答案为:
| 2 |
| sinθ |
点评:本题考查三角函数的化简求值,考查平方关系的应用,属于中档题.

练习册系列答案
相关题目
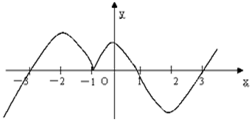 已知函数y=f(x)的导函数y=f′(x)图象如图所示
已知函数y=f(x)的导函数y=f′(x)图象如图所示