题目内容
设数列{an}的前n项和为Sn,数列{Sn}的前n项和为Tn,且满足Tn=
Sn-3n,n∈N*.
(1)求a1的值;
(2)求数列{an}的通项公式;
(3)记bn=
,n∈N*,求证:b1+b2+…+bn<1.
| 3 |
| 2 |
(1)求a1的值;
(2)求数列{an}的通项公式;
(3)记bn=
| 2an |
| (an-2)2 |
考点:数列的求和,数列递推式
专题:综合题
分析:(1)将n=1代入Tn=
Sn-3n,求出a1的值;
(2)根据当n≥2时,Sn=Tn-Tn-1求出Sn=
an-3仿写作差得出数列{an}是以6为首项,3为公比的等比数列,求出通项公式;
(3)当n=1时,b1=
<1;当n≥2时,bn=
=
=
<
=
(
-
)通过裂项相消证出不等式.
| 3 |
| 2 |
(2)根据当n≥2时,Sn=Tn-Tn-1求出Sn=
| 3 |
| 2 |
(3)当n=1时,b1=
| 3 |
| 4 |
| 2an |
| (an-2)2 |
| 4×3n | ||
(2×3n-2)2
|
| 3n |
| (3n-1)2 |
| 3n |
| (3n-1)(3n-3) |
| 1 |
| 2 |
| 1 |
| 3n-1-1 |
| 1 |
| 3n-1 |
解答:
解:(1)当n=1时,T1=
S1-3,
∵T1=S1=a1
,∴a1=
a1-3
解得a1=6
(2)当n≥2时,Sn=Tn-Tn-1=
Sn-3n-[
Sn-1-3(n-1)]=
Sn-
Sn-1-3
∴Sn=
an-3①
∴Sn-1=
an-1-3①
由②-①得an=3an-1
∴数列{an}是以6为首项,3为公比的等比数列
,∴an=6•3n-1=2•3n
(3)当n=1时,b1=
<1
当n≥2时,bn=
=
=
<
=
=
[
]
=
(
-
)
∴b1+b2+…+bn<b1+
(
-
)+
(
-
)+…+
(
-
)
<
+
(
-
)<1
| 3 |
| 2 |
∵T1=S1=a1
,∴a1=
| 3 |
| 2 |
解得a1=6
(2)当n≥2时,Sn=Tn-Tn-1=
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∴Sn=
| 3 |
| 2 |
∴Sn-1=
| 3 |
| 2 |
由②-①得an=3an-1
∴数列{an}是以6为首项,3为公比的等比数列
,∴an=6•3n-1=2•3n
(3)当n=1时,b1=
| 3 |
| 4 |
当n≥2时,bn=
| 2an |
| (an-2)2 |
| 4×3n |
| (2×3n-2)2 |
| 3n |
| (3n-1)2 |
| 3n |
| (3n-1)(3n-3) |
=
| 3n-1 |
| (3n-1)(3n-1-1) |
| 1 |
| 2 |
| (3n-1)-(3n-1-1) |
| (3n-1)(3n-1-1) |
=
| 1 |
| 2 |
| 1 |
| 3n-1-1 |
| 1 |
| 3n-1 |
∴b1+b2+…+bn<b1+
| 1 |
| 2 |
| 1 |
| 31-1 |
| 1 |
| 32-1 |
| 1 |
| 2 |
| 1 |
| 32-1 |
| 1 |
| 33-1 |
| 1 |
| 2 |
| 1 |
| 3n-1-1 |
| 1 |
| 3n-1 |
<
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3-1 |
| 1 |
| 3n-1 |
点评:本题考查数列通项的求法、考查了放缩法证明不等式及裂项相消的数列求和的方法;属于一道综合题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
半径为R的球O中有一内接圆柱,当圆柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是( )
| A、πR2 |
| B、2πR2 |
| C、3πR2 |
| D、4πR2 |
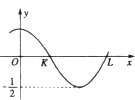 设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,KL=1,则f(
设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,KL=1,则f(| 1 |
| 6 |
A、-
| ||||
B、-
| ||||
C、-
| ||||
D、
|
 高三某班20名男生在一次体检中被平均分成两个小组,第一组和第二组学生身高(单位:cm)的统计数据用茎叶图表示,如图所示.
高三某班20名男生在一次体检中被平均分成两个小组,第一组和第二组学生身高(单位:cm)的统计数据用茎叶图表示,如图所示.