题目内容
已知函数f(x)=
sin2x-cos2x+
,x∈R.
(Ⅰ)若x∈[
π,
π],求函数f(x)的最大值和最小值及相应的x的值;
(Ⅱ)设△ABC的内角A、B、C的对边分别为a、b、c,c=
,f(C)=1,且sinB=2sinA,求a、b的值.
| ||
| 2 |
| 1 |
| 2 |
(Ⅰ)若x∈[
| 5 |
| 24 |
| 3 |
| 4 |
(Ⅱ)设△ABC的内角A、B、C的对边分别为a、b、c,c=
| 3 |
考点:三角函数中的恒等变换应用,余弦定理
专题:三角函数的图像与性质
分析:(Ⅰ)首先,借助于二倍角公式,化简函数解析式:f(x)=sin(2x-
),然后,结合x∈[
π,
π]进行求解;
(Ⅱ)根据f(C)=1,得到C=
,然后,结合正弦定理和余弦定理进行求解.
| π |
| 6 |
| 5 |
| 24 |
| 3 |
| 4 |
(Ⅱ)根据f(C)=1,得到C=
| π |
| 3 |
解答:
解:(Ⅰ)∵函数f(x)=
sin2x-cos2x+
,
∴f(x)=
sin2x-
+
=sin(2x-
),
∴f(x)=sin(2x-
),
∵x∈[
π,
π],
∴(2x-
)∈[
,
],
∴当2x-
=
,即x=
时,f(x)max=1,
∴当2x-
=
,即x=
时,f(x)min=-
;
(Ⅱ)∵f(C)=sin(2C-
)=1,
∴sin(2C-
)=1,
∵0<C<π,
∴-
<2C-
<
,
∴2C-
=
,
∴C=
,
∵sinB=2sinA,
∴根据正弦定理,得b=2a,①
根据余弦定理,得c2=a2+b2-2abcos
,
∴c2=a2+b2-ab,②
根据①②,解得a=1,b=2.
| ||
| 2 |
| 1 |
| 2 |
∴f(x)=
| ||
| 2 |
| 1+cos2x |
| 2 |
| 1 |
| 2 |
=sin(2x-
| π |
| 6 |
∴f(x)=sin(2x-
| π |
| 6 |
∵x∈[
| 5 |
| 24 |
| 3 |
| 4 |
∴(2x-
| π |
| 6 |
| π |
| 4 |
| 4π |
| 3 |
∴当2x-
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
∴当2x-
| π |
| 6 |
| 4π |
| 3 |
| 3π |
| 4 |
| ||
| 2 |
(Ⅱ)∵f(C)=sin(2C-
| π |
| 6 |
∴sin(2C-
| π |
| 6 |
∵0<C<π,
∴-
| π |
| 6 |
| π |
| 6 |
| 11π |
| 6 |
∴2C-
| π |
| 6 |
| π |
| 2 |
∴C=
| π |
| 3 |
∵sinB=2sinA,
∴根据正弦定理,得b=2a,①
根据余弦定理,得c2=a2+b2-2abcos
| π |
| 3 |
∴c2=a2+b2-ab,②
根据①②,解得a=1,b=2.
点评:.本题重点考查了三角恒等变换、三角函数、正弦定理、余弦定理等知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
INPUT a
b=a\10-a/10+aMOD10
PRINT b
END
若a=35,则以上程序运行的结果是( )
b=a\10-a/10+aMOD10
PRINT b
END
若a=35,则以上程序运行的结果是( )
| A、4.5 | B、3 | C、1.5 | D、2 |
若向量
=(1,2),
=(4,x),且
与
共线,则
=( )
| BA |
| CA |
| BA |
| CA |
| BC |
| A、(-3,-6) |
| B、(3,6) |
| C、(5,10) |
| D、(-3,4) |
 如图,矩形ABCD所在的平面与平面ABF互相垂直,在△ABF中,AB=
如图,矩形ABCD所在的平面与平面ABF互相垂直,在△ABF中,AB=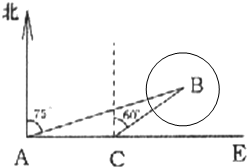 如图,海中有一小岛B,周围3.8海里内有暗礁.一军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北偏东60°.
如图,海中有一小岛B,周围3.8海里内有暗礁.一军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北偏东60°.