题目内容
已知函数y=
.
(1)求函数f(x)图象的对称中心;
(2)判断函数f(
)的单调性,并证明你的结论;
(3)e为自然对数的底数,求函数f(ex)-f(e-x)的值域.
| 2x-1 |
| x+1 |
(1)求函数f(x)图象的对称中心;
(2)判断函数f(
| x |
(3)e为自然对数的底数,求函数f(ex)-f(e-x)的值域.
考点:函数单调性的判断与证明,函数的值域,奇偶函数图象的对称性
专题:函数的性质及应用
分析:(1)化简函数y,求出它的函数图象的对称中心;
(2)求出f(
),用定义证明它的单调性;
(3)求出f(ex)-f(e-x),根据(2)的结论求出f(ex)-f(e-x)的值域.
(2)求出f(
| x |
(3)求出f(ex)-f(e-x),根据(2)的结论求出f(ex)-f(e-x)的值域.
解答:
解:(1)∵函数y=
=2-
,x+1≠0,
∴x≠-1,∴y≠2,
∴f(x)图象的对称中心是(-1,2);
(2)f(
)=2-
(x≥0)是定义域上的增函数;
证明:任取x1、x2∈[0,+∞),且x1<x2,
∴f(x1)-f(x2)=(2-
)-(2-
)
=
=
;
∵0≤x1<x2,∴x1-x2<0,
+
>0,
+1>0,
+1>0;
∴f(x1)-f(x2)<0,即f(x1)<f(x2);
∴f(x)是定义域上的增函数;
(3)∵f(ex)-f(e-x)=(2-
)-(2-
)
=
=3-
;
由(2)知它是定义域上的增函数,且ex∈(0,+∞),
∴f(ex)-f(e-x)的值域是(-1,3).
| 2x-1 |
| x+1 |
| 3 |
| x+1 |
∴x≠-1,∴y≠2,
∴f(x)图象的对称中心是(-1,2);
(2)f(
| x |
| 3 | ||
|
证明:任取x1、x2∈[0,+∞),且x1<x2,
∴f(x1)-f(x2)=(2-
| 3 | ||
|
| 3 | ||
|
=
3(
| ||||
(
|
=
| 3(x1-x2) | ||||||||
(
|
∵0≤x1<x2,∴x1-x2<0,
| x1 |
| x2 |
| x1 |
| x2 |
∴f(x1)-f(x2)<0,即f(x1)<f(x2);
∴f(x)是定义域上的增函数;
(3)∵f(ex)-f(e-x)=(2-
| 3 |
| ex+1 |
| 3 |
| e-x+1 |
=
| 3(ex-1) |
| ex+1 |
=3-
| 4 |
| ex+1 |
由(2)知它是定义域上的增函数,且ex∈(0,+∞),
∴f(ex)-f(e-x)的值域是(-1,3).
点评:本题考查了求函数图象的对称中心,判定函数的单调性,以及求函数的值域的问题,解题时应认真分析,逐层深入,进行解答,是综合性题目.

练习册系列答案
相关题目
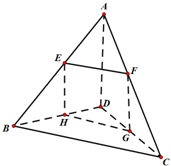 空间四边形ABCD中,AD=BC=a,与直线AD,BC都平行的平面分别交AB,AC,CD,BD于E,F,H.
空间四边形ABCD中,AD=BC=a,与直线AD,BC都平行的平面分别交AB,AC,CD,BD于E,F,H. 如图,已知底面为菱形的四棱锥P-ABCD中,△ABC是边长为2的正三角形,AP=BP=
如图,已知底面为菱形的四棱锥P-ABCD中,△ABC是边长为2的正三角形,AP=BP=