题目内容
已知△ABC中,内角A,B,C的对边分别为a,b,c,向量
=(
cosB,
sinB),向量
=(cosc,-sinc),若|
-
|=
.
(1)求角A的大小;
(2)若a=4
,且△ABC的面积为16,求b,c.
| m |
| 2 |
| 2 |
| n |
| m |
| n |
| 5 |
(1)求角A的大小;
(2)若a=4
| 2 |
考点:余弦定理,平面向量数量积的运算,正弦定理
专题:解三角形
分析:(1)由向量的模长可得cos(B+C)=-
,由诱导公式可得cosA=
,由A的范围可得;
(2)由余弦定理可得(4
)2=b2+c2-2bccos
,由面积公式可得S=
bcsin
=16,化简联立方程组解之可得答案.
| ||
| 2 |
| ||
| 2 |
(2)由余弦定理可得(4
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 4 |
解答:
解:(1)∵
=(
cosB,
sinB),
=(cosc,-sinc),
∴|
-
|=(
cosB-cosC,
sinB+sinc),
又∵|
-
|=
,∴(
cosB-cosC)2+(
sinB+sinc)2=5,
展开化简可得-
(cosBcosC-sinBsinC)=1,
∴cos(B+C)=-
,∴cosA=-cos(B+C)=
,
∵A∈(0,π),∴A=
(2)由余弦定理可得(4
)2=b2+c2-2bccos
,
化简可得32=b2+c2-
bc,①
又△ABC的面积为S=
bcsin
=16,即
bc=64,②
把②①代入①可得b2+c2=96,③
联立①③可解得b=8,c=4
,或b=4
,c=8
| m |
| 2 |
| 2 |
| n |
∴|
| m |
| n |
| 2 |
| 2 |
又∵|
| m |
| n |
| 5 |
| 2 |
| 2 |
展开化简可得-
| 2 |
∴cos(B+C)=-
| ||
| 2 |
| ||
| 2 |
∵A∈(0,π),∴A=
| π |
| 4 |
(2)由余弦定理可得(4
| 2 |
| π |
| 4 |
化简可得32=b2+c2-
| 2 |
又△ABC的面积为S=
| 1 |
| 2 |
| π |
| 4 |
| 2 |
把②①代入①可得b2+c2=96,③
联立①③可解得b=8,c=4
| 2 |
| 2 |
点评:本题考查正余弦定理的应用,涉及向量的模长公式,属中档题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 如图,在正三棱柱ABC-A1B1C1中,AA1=3,底面边长为
如图,在正三棱柱ABC-A1B1C1中,AA1=3,底面边长为 在如图1的等腰梯形ABCD中,AB=1,DC=3,DA=BC=
在如图1的等腰梯形ABCD中,AB=1,DC=3,DA=BC=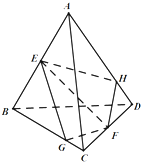 如图,在四面体ABCD中,E,F分别为AB,CD的中点,过EF任作一个平面α分别与直线BC,AD相交于点G,H,则下列结论正确的是
如图,在四面体ABCD中,E,F分别为AB,CD的中点,过EF任作一个平面α分别与直线BC,AD相交于点G,H,则下列结论正确的是