题目内容
f(x)=asin3x+b3
cos3x+4,f(sin10°)=5,则f(cos100°)= .
| x |
考点:函数奇偶性的性质,运用诱导公式化简求值
专题:函数的性质及应用
分析:f(x)=asin3x+b3
cos3x+4,可得f(-x)+f(x)=8,因此f(sin10°)+f(-sin10°)=8.而f(cos100°)=f(-sin10°),即可得出.
| x |
解答:
解:∵f(x)=asin3x+b3
cos3x+4,
∴f(-x)+f(x)=8,
∴f(sin10°)+f(-sin10°)=8.
∴f(-sin10°)=8-5=3.
∴f(cos100°)=f(-sin10°)=3.
故答案为:3.
| x |
∴f(-x)+f(x)=8,
∴f(sin10°)+f(-sin10°)=8.
∴f(-sin10°)=8-5=3.
∴f(cos100°)=f(-sin10°)=3.
故答案为:3.
点评:本题考查了函数的奇偶性、三角函数求值、诱导公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
命题“x2-9=0的解是x=±3”,在这个命题中,使用的逻辑联结词的情况是( )
| A、没有使用逻辑联结词 |
| B、使用了“且” |
| C、使用了“或” |
| D、使用了“非” |
下列说法正确的是( )
| A、若p∧q为假命题,则p、q都为假命题 | ||||||||
| B、“f(0)=0”是“函数f(x)为奇函数”充要条件 | ||||||||
| C、若命题p:?x0∈R,2x02+x0+3>0,则?p:?x∈R,2x2+x+3<0 | ||||||||
D、若“a=
|
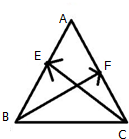 如图,在边长为2的正△ABC中,E、F分别是AB、AC的中点,求
如图,在边长为2的正△ABC中,E、F分别是AB、AC的中点,求