题目内容
对于定义域为D的函数y=f(x),若同时满足下列条件:
①f(x)在D内具有单调性;
②存在区间[a,b]⊆D,使f(x)在[a,b]上的值域为[a,b];那么称y=f(x)(x∈D)为闭函数.
(1)求闭函数y=-x3符合条件②的区间[a,b];
(2)判断函数f(x)=
x+
(x>0)是否为闭函数?并说明理由;
(3)若函数y=k+
是闭函数,求实数k的取值范围.
①f(x)在D内具有单调性;
②存在区间[a,b]⊆D,使f(x)在[a,b]上的值域为[a,b];那么称y=f(x)(x∈D)为闭函数.
(1)求闭函数y=-x3符合条件②的区间[a,b];
(2)判断函数f(x)=
| 3 |
| 5 |
| 2 |
| x |
(3)若函数y=k+
| x+1 |
考点:函数与方程的综合运用,函数的定义域及其求法,函数的值域,函数的零点与方程根的关系
专题:函数的性质及应用
分析:(1)利用闭函数的定义,判断y=-x3符合条件②时满足的关系式,即可求解区间[a,b];
(2)判断函数f(x)=
x+
(x>0)是否为单调函数即可判断是否为闭函数;
(3)利用函数y=k+
是闭函数,利用函数的单调性列出不等式组,即可求实数k的取值范围.
(2)判断函数f(x)=
| 3 |
| 5 |
| 2 |
| x |
(3)利用函数y=k+
| x+1 |
解答:
解:(1)∵f(0)>f(1)且f(x)为闭函数
∴f(x)=-x3在R上单调减,…(1分)
∴
即
…(4分)
∴符合条件的闭区间为[-1,1]…(5分)
(2)解:函数f(x)=
x+
,所以函数f′(x)=
-
,显然导函数有两个零点,一个大于0,所以函数在(0,+∞)上不是单调函数,不满足闭函数的定义. …(10分)
(3)解:∵f(x)是闭函数且在[a,b]上单调增
∴
∴a,b是方程k+
=x的两个不等实根…(12分)
令t=
∴t2-t-k-1=0在[0,+∞)上有两个不相等实根
∴
…(15分)
∴-
<k≤-1…(16分)
∴f(x)=-x3在R上单调减,…(1分)
∴
|
|
|
∴符合条件的闭区间为[-1,1]…(5分)
(2)解:函数f(x)=
| 3 |
| 5 |
| 2 |
| x |
| 3 |
| 5 |
| 2 |
| x2 |
(3)解:∵f(x)是闭函数且在[a,b]上单调增
∴
|
∴a,b是方程k+
| x+1 |
令t=
| x+1 |
∴
|
∴-
| 5 |
| 4 |
点评:本题考查新定义的应用,函数的导数判断函数的单调性以及转化思想的应用,考查分析问题解决问题的能力.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
已知函数f(x)=
,则f(-10)的值是( )
|
| A、-2 | B、-1 | C、0 | D、1 |
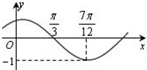 函数f(x)=Acos(ωx+φ)(A>0,ω>0)的图象如图所示,为了得到g(x)=Acosωx的图象,可以将f(x)的图象( )
函数f(x)=Acos(ωx+φ)(A>0,ω>0)的图象如图所示,为了得到g(x)=Acosωx的图象,可以将f(x)的图象( )A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
以直线x-2y=0和x+2y-4=0的交点为圆心,且过点(2,0)的圆的方程为( )
| A、(x-2)2+(y-1)2=1 |
| B、(x+2)2+(y+1)2=1 |
| C、(x-2)2+(y-1)2=2 |
| D、(x+2)2+(y+1)2=2 |