题目内容
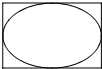如图所示，矩形长为3，宽为2，在矩形内随机撒200颗黄豆，数得落在椭圆内的黄豆数为160颗，依据此实验数据可以估计出椭圆的面积约为（ ）| A、4.7 | B、4.8 |
| C、1.2 | D、1.3 |
考点：几何概型
专题：概率与统计
分析：欲估计出椭圆的面积，可利用几何概型的概率模拟，只要利用椭圆的面积与矩形面积的比与落在椭圆内的黄豆数与所有黄豆数的比．
解答：
解：∵黄豆落在椭圆内的概率为：
=
即：
=
解得：S椭圆=4.8．
故选B．
| 椭圆面积 |
| 矩形面积 |
| 160 |
| 200 |
即：
| S椭圆 |
| 3×2 |
| 160 |
| 200 |
解得：S椭圆=4.8．
故选B．
点评：本题考查几何概型的应用（用来估计不规则图象的面积等）．如果每个事件发生的概率只与构成该事件区域的长度（面积或体积）成比例，则称这样的概率模型为几何概率模型，称为几何概型．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
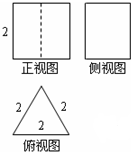已知一个空间几何体的三视图如图所示，且这个空间几何体的所有顶点都在一个球面上，则球的表面积是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
已知变量x，y，满足约束条件
，则z=3x+y的取值范围为（ ）
|
| A、[-12，3] | ||
| B、[3，12] | ||
C、[-12，
| ||
D、[-
|
阅读如图所示的程序框图，输出的结果S的值为（ ）
| A、0 | ||||
B、
| ||||
C、
| ||||
D、-
|