题目内容
直线3x+4y+11=0与圆(x-1)2+(y+1)2=1的位置关系为( )
| A、过圆心 | B、相离 | C、相切 | D、相交 |
考点:圆与圆的位置关系及其判定
专题:直线与圆
分析:求出圆的圆心与半径,利用圆心到直线的距离与半径比较,即可得到选项.
解答:
解:圆(x-1)2+(y+1)2=1的圆心坐标(1,-1),半径为:1.
圆心到直线的距离为:
=2>1.
圆与直线相离.
故选:B.
圆心到直线的距离为:
| |3-4+11| | ||
|
圆与直线相离.
故选:B.
点评:本题考查直线与圆的位置关系的应用,基本知识的考查.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
由曲线y=
与直线x=1,及x=4围成的图形的面积等于( )
| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
双曲线
-
=1(a>0,b>0)的两条渐近线与抛物线y=x2+1有四个公共点,则该双曲线的离心率的取值范围是( )
| y2 |
| a2 |
| x2 |
| b2 |
A、(1,
| ||||
B、(1,
| ||||
C、(
| ||||
D、(
|
已知
=(-3,4)与
=(6,x)共线,则x=( )
| a |
| b |
| A、8 | ||
| B、-8 | ||
C、
| ||
D、-
|
正方体ABCD-A1B1C1D1中,二面角A-BD1-B1的大小为( )
| A、90° | B、60° |
| C、120° | D、45° |
如果25,x,y,z,1成等比数列,那么( )
| A、y=5,xz=25 |
| B、y=-5,xz=25 |
| C、y=5,xz=-25 |
| D、y=-5,xz=-25 |
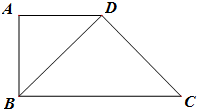 如图,梯形ABCD中,AD∥BC,AD=AB=1,AD⊥AB,∠BCD=45°,将△ABD沿对角线BD折起.设折起后点A的位置为A′,并且平面A′BD⊥平面BCD.给出下面四个命题:
如图,梯形ABCD中,AD∥BC,AD=AB=1,AD⊥AB,∠BCD=45°,将△ABD沿对角线BD折起.设折起后点A的位置为A′,并且平面A′BD⊥平面BCD.给出下面四个命题: