题目内容
正方体ABCD-A1B1C1D1中,二面角A-BD1-B1的大小为( )
| A、90° | B、60° |
| C、120° | D、45° |
考点:二面角的平面角及求法
专题:空间角
分析:设正方体ABCD-A1B1C1D1的棱长为1,以D为原点建立空间直角坐标系D-xyz,利用向量法能求出二面角A-BD1-B1的大小为120°.
解答:
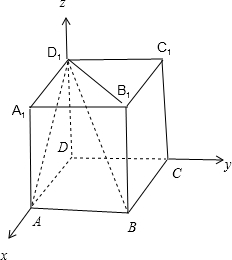 解:设正方体ABCD-A1B1C1D1的棱长为1,
解:设正方体ABCD-A1B1C1D1的棱长为1,
以D为原点建立空间直角坐标系D-xyz,
A(1,0,0),B(1,1,0),D1(0,0,1),B1(1,1,1),
=(0,1,0),
=(-1,-1,1),
=(0,0,1),
设平面ABD1的法向量
=(x,y,z),
则
,取x=1,得
=(1,0,1),
设平面B1BD1的法向量
=(a,b,c),
则
,取a=1,得
=(1,-1,0),
设二面角A-BD1-B1的平面角为θ,
cosθ=-|cos<
,
>|=-
,
∴二面角A-BD1-B1的大小为120°.
故选:C.
 解:设正方体ABCD-A1B1C1D1的棱长为1,
解:设正方体ABCD-A1B1C1D1的棱长为1,以D为原点建立空间直角坐标系D-xyz,
A(1,0,0),B(1,1,0),D1(0,0,1),B1(1,1,1),
| BA |
| BD1 |
| BB1 |
设平面ABD1的法向量
| n |
则
|
| n |
设平面B1BD1的法向量
| m |
则
|
| m |
设二面角A-BD1-B1的平面角为θ,
cosθ=-|cos<
| m |
| n |
| 1 |
| 2 |
∴二面角A-BD1-B1的大小为120°.
故选:C.
点评:本题考查二面角的大小的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
函数f(x)=
-2sinπx在区间[-2,4]上的所有零点之和等于( )
| 1 |
| 1-x |
| A、2 | B、6 | C、8 | D、10 |
已知不等式组
,表示的三角形区域为M,过该区域三顶点的圆内部记为N,在N中随机取一点,则该点取自区域M的概率为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
对任意的锐角α,β下列不等关系中正确的是( )
| A、sin(α+β)>sinα+sinβ |
| B、sin(α+β)>cosα+cosβ |
| C、cos(α+β)<cosα+sinβ |
| D、cos(α+β)>sinα+sinβ |
直线3x+4y+11=0与圆(x-1)2+(y+1)2=1的位置关系为( )
| A、过圆心 | B、相离 | C、相切 | D、相交 |
若a-b<0,则下列各式中一定成立的是( )
| A、ac<bc | ||||
| B、-a>-b | ||||
C、
| ||||
| D、a2<b2 |
若点P(x,y)在椭圆
+
=1上,则x的范围是( )
| x2 |
| 4 |
| y2 |
| 3 |
| A、[-4,4] | ||||
| B、[-2,2] | ||||
| C、[-3,3] | ||||
D、[-
|