题目内容
解关于x的不等式：
＞0．
| 2x2-x+1 |
| 2x+1 |
考点：其他不等式的解法
专题：不等式的解法及应用
分析：根据2x2-x+1的判别式△＜0，可得2x2-x+1＞0恒成立．故由原不等可得2x+1＞0，由此求得它的解集．
解答：
解：关于x的不等式：
＞0，由于2x2-x+1的判别式△=-7＜0，∴2x2-x+1＞0恒成立．
故由原不等可得2x+1＞0，求得它的解集为{x|x＞-
}．
| 2x2-x+1 |
| 2x+1 |
故由原不等可得2x+1＞0，求得它的解集为{x|x＞-
| 1 |
| 2 |
点评：本题主要考查分式不等式的解法，一元二次不等式的解法，体现了等价转化的数学思想，属于基础题．
练习册系列答案
相关题目
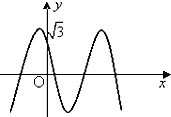如图，函数f（x）=2cos（ωx+θ）（x∈R，ω＞0，0≤θ≤
已知函数y=Asin（ωx+φ）（A＞0，|φ|＜π）的一段图象如图所示，则函数的解析式为