题目内容
长方体的表面积是24,所有棱长的和是24,则对角线的长是( )
A、
| ||
| B、4 | ||
C、3
| ||
D、2
|
考点:棱柱、棱锥、棱台的体积,棱柱的结构特征,棱柱、棱锥、棱台的侧面积和表面积
专题:空间位置关系与距离
分析:设出长方体的长、宽、高,表示出长方体的全面积,十二条棱长度之和,然后可得对角线的长度.
解答:
解:设长方体的长、宽、高分别为a,b,c,由题意可知,
,
由①的平方减去②可得a2+b2+c2=12,
这个长方体的一条对角线长为:2
,
故选:D.
|
由①的平方减去②可得a2+b2+c2=12,
这个长方体的一条对角线长为:2
| 3 |
故选:D.
点评:本题考查长方体的结构特征,面积和棱长的关系,考查计算能力及方程思想,是基础题.

练习册系列答案
相关题目
在棱长为a的正方体ABCD-A1B1C1D1中,错误的是( )
| A、直线A1B和直线AC所成角的大小为60° | ||
| B、直线AC∥平面DA1C1 | ||
C、二面角B-AB1-C的大小是arctan
| ||
| D、直线A1B1到平面ABC1D1的距离为a |
若a<b<0,则下列不等式成立的是( )
| A、a2<b2 |
| B、a2≤b2 |
| C、a-b>0 |
| D、|a|>|b| |
双曲线x2-y2=2的顶点到其渐进线的距离等于( )
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
已知
-
=-8
+16
,
+
=2
-8
(
,
为互相垂直的单位向量),则
•
=( )
| a |
| b |
| i |
| j |
| a |
| b |
| i |
| j |
| i |
| j |
| a |
| b |
| A、63 | B、-63 |
| C、33 | D、-33 |
将一个白球,两个相同的红球,三个相同的黄球摆放成一排.则白球与黄球不相邻的放法有( )
| A、10种 | B、12种 |
| C、14种 | D、16种 |
已知向量
=(1,0),
=(-
,
),则
与
的夹角为( )
| a |
| b |
| 1 |
| 2 |
| ||
| 2 |
| a |
| b |
| A、30° | B、60° |
| C、120° | D、150° |
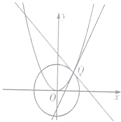 如图,抛物线C:x2=2py与圆O:x2+y2=1在第一象限的交点为Q,圆O和抛物线C在点Q处的切线的斜率分别为k1,k2,若k1+k2=1,则p=
如图,抛物线C:x2=2py与圆O:x2+y2=1在第一象限的交点为Q,圆O和抛物线C在点Q处的切线的斜率分别为k1,k2,若k1+k2=1,则p=