题目内容
等比数列{an}的前n项和为Sn，若a1+a2+a3=3，a4+a5+a6=6，则S12=（ ）
| A、15 | B、30 | C、45 | D、60 |
考点：等比数列的前n项和
专题：等差数列与等比数列
分析：等比数列{an}中，Sm，S2m-Sm，S3m-S2m也成等比数列，由此利用已知条件能求出S12．
解答：
解：等比数列{an}中，
∵a1+a2+a3=3，a4+a5+a6=6，
∴a7+a8+a9=2×6=12，
a10+a11+a12=2×12=24，
∴S12=3+6+12+24=45．
故答案为：45．
∵a1+a2+a3=3，a4+a5+a6=6，
∴a7+a8+a9=2×6=12，
a10+a11+a12=2×12=24，
∴S12=3+6+12+24=45．
故答案为：45．
点评：本题考查等比数列的前12项的和的求法，是基础题，解题时要认真审题，注意等比数列的性质的灵活运用．
练习册系列答案
相关题目
若对数函数y=logax在（0，+∞）上是减函数，那么（ ）
| A、0＜a＜1 | B、-1＜a＜0 |
| C、a=-1 | D、a＜-1 |
下面四个条件中，使a＞b成立的充分而不必要的条件是（ ）
| A、a2＞b2 |
| B、a3＞b3 |
| C、a＞b+1 |
| D、a＞b-1 |
已知命题p：?x∈R，使得x+
＜2，命题q：?x∈R，x2+x+1＞0，下列命题为真的是（ ）
| 1 |
| x |
| A、p∧q |
| B、（￢p）∧q |
| C、p∧（￢q） |
| D、（￢p）∧（￢q） |
设函数f（x）的导函数为f′（x），且f（x）=x2+2x•f′（1），则f′（1）=（ ）
| A、0 | B、-4 | C、-2 | D、2 |
直线L1过点A（m，1）和点B（-1，m），直线L2过点C（m+n，n+1）和点D（n+1，n-m）．则直线L1与L2的位置关系是（ ）
| A、重合 | B、平行 |
| C、垂直 | D、无法确定 |
“直线l与平面α内无数条直线都垂直”是“直线l与平面α垂直”的（ ）条件．
| A、必要非充分 |
| B、充分非必要 |
| C、充要 |
| D、既非充分又非必要 |
已知实数a，b，则a+b＞0是a＞0且b＞0的（ ）条件．
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分也不必要 |
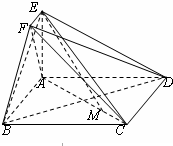在如图所示的几何体中，四边形ABCD为正方形，EA⊥平面ABCD，EF∥AB，AB=4，AE=2，EF=1．