题目内容
椭圆
+
=
的离心率是
，它被直线x-y-1=0截得的弦长是
，求椭圆的方程．
| x2 |
| a2 |
| y2 |
| b2 |
|
| ||
| 3 |
8
| ||
| 5 |
考点：椭圆的标准方程
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据椭圆
+
=
的离心率是
，可得a，c的关系，利用被直线x-y-1=0截得的弦长是
，根据韦达定理，即可求椭圆的方程．
| x2 |
| a2 |
| y2 |
| b2 |
|
| ||
| 3 |
8
| ||
| 5 |
解答：
解：∵e=
=
，即
=
，∴a2=3c2
∴b2=a2-c2=2c2，∴椭圆方程可写为
+
=1…（2分）
将直线方程x-y-1=0代入椭圆方程，消去y，整理得5x2-6x+3-6c2=0，
依韦达定理得x1+x2=
，x1x2=
…（6分）
∴
=
|x1-x2|=
•
=
•
=
解得c=1，
∴a2=3，b2=2，
∴椭圆方程为
+
=1…（12分）
| c |
| a |
| ||
| 3 |
| c2 |
| a2 |
| 1 |
| 3 |
∴b2=a2-c2=2c2，∴椭圆方程可写为
| x2 |
| 3c2 |
| y2 |
| 2c2 |
将直线方程x-y-1=0代入椭圆方程，消去y，整理得5x2-6x+3-6c2=0，
依韦达定理得x1+x2=
| 6 |
| 5 |
| 3-6c2 |
| 5 |
∴
8
| ||
| 5 |
| 1+12 |
| 2 |
| (x1+x2)2-4x1x2 |
| 2 |
(
|
| ||
| 5 |
解得c=1，
∴a2=3，b2=2，
∴椭圆方程为
| x2 |
| 3 |
| y2 |
| 2 |
点评：本题考查椭圆的标准方程，考查直线与椭圆的位置关系，考查韦达定理的运用，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
如图是一个几何体的三视图，则这个几何体是（ ）
| A、圆柱 | B、圆台 | C、圆锥 | D、棱台 |
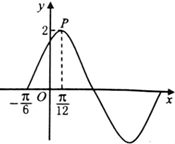已知函数f（x）=Asin（ωx+φ），（ω＞0，A＞0，φ∈（0，
