题目内容
解关于x的不等式:
≥2logax+3.
| 2 |
| 1-logax |
考点:其他不等式的解法
专题:不等式的解法及应用
分析:根据分式不等式的解法,讨论分母的符号,将不等式进行转换,然后利用对数不等式的解法即可得到结论.
解答:
解:①若1-logax>0,
即logax<1时,
则不等式等价为2≥(2logax+3)(1-logax),
即2(logax)2+logax-1≥0,
解得logax≤-1或logax≥
,
即logax≤-1或
≤logax<1.
②若1-logax<0,
即logax>1时,
则不等式等价为2≤(2logax+3)(1-logax),
即2(logax)2+logax-1≤0,
解得:-1≤logax≤
,
此时不等式无解.
综上:logax≤-1或
≤logax<1.
若a>1,则0<x≤
,或
≤x<a,
若0<a<1,则x≥
,或a<x≤
,
综上述,若a>1,不等式的解集为:{x|0<x≤
,或
≤x<a},
若0<a<1,不等式的解集为:{x|x≥
,或a<x≤
}.
即logax<1时,
则不等式等价为2≥(2logax+3)(1-logax),
即2(logax)2+logax-1≥0,
解得logax≤-1或logax≥
| 1 |
| 2 |
即logax≤-1或
| 1 |
| 2 |
②若1-logax<0,
即logax>1时,
则不等式等价为2≤(2logax+3)(1-logax),
即2(logax)2+logax-1≤0,
解得:-1≤logax≤
| 1 |
| 2 |
此时不等式无解.
综上:logax≤-1或
| 1 |
| 2 |
若a>1,则0<x≤
| 1 |
| a |
| a |
若0<a<1,则x≥
| 1 |
| a |
| a |
综上述,若a>1,不等式的解集为:{x|0<x≤
| 1 |
| a |
| a |
若0<a<1,不等式的解集为:{x|x≥
| 1 |
| a |
| a |
点评:本题主要考查分式不等式的解法,利用分类讨论的思想是解决本题的关键,注意要利用好对数函数的单调性的性质.考查学生的计算能力.

练习册系列答案
相关题目
“x<-1”是“x<0”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
如图是一个几何体的三视图,则这个几何体是( )


| A、圆柱 | B、圆台 | C、圆锥 | D、棱台 |
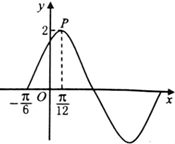 已知函数f(x)=Asin(ωx+φ),(ω>0,A>0,φ∈(0,
已知函数f(x)=Asin(ωx+φ),(ω>0,A>0,φ∈(0,