题目内容
已知函数f（x）=x|x+a|-
lnx．
（1）若a＞0，求函数f（x）的极值点；
（2）若f（x）＞0，求a取值范围．
| 1 |
| 2 |
（1）若a＞0，求函数f（x）的极值点；
（2）若f（x）＞0，求a取值范围．
考点：利用导数研究函数的极值
专题：导数的综合应用
分析：（1）先求出函数的导数，再找到单调区间，从而找到极值点；
（2）x＞0，由f（x）＞0得|x+a|＞
，分别讨论当①0＜x＜1，
＜0，得a∈R，②当x=1，|1+a|＞0得a≠-1，③当x＞1时的情况，从而求出a的范围．
（2）x＞0，由f（x）＞0得|x+a|＞
| lnx |
| 2x |
| lnx |
| 2x |
解答：
解：（1）a＞0，x＞0，f(x)=x2+ax-
lnx，
f′(x)=2x+a-
=
，
f′(x)=0⇒x1=
＜0，x2=
＞0，
f'（x）＜0⇒x∈（0，x2）减函数，f'（x）＞0⇒x∈（x2，+∞）增函数，
∴x2=
是函数的极小值点，无极大值点．
（2）x＞0，由f（x）＞0得|x+a|＞
，
当0＜x＜1，
＜0，得a∈R，
当x=1，|1+a|＞0得a≠-1，
当x＞1，不等比等价于a＜-x-
，或a＞-x+
令g(x)=-x-
，h′(x)=-1-
=
令φ（x）=-2x2-1+lnx，
φ′(x)=-4x+
=
＜0(x＞1)，
φ（x）在（1，+∞）减函数，φ（x）＜φ（1）=-3＜0，
得g（x）在（1，+∞）减函数，g（x）∈（-∞，-1），
∴a＜-x-
不恒成立．
又令h(x)=-x+
，
∴h′(x)=-1+
=
令ψ（x）=-2x2+1-lnx在（1，+∞）减函数，ψ（x）＜ψ（1）=-1＜0，
得h（x）在（1，+∞）是减函数，h（x）＜h（1）=-1，得a≥-1．
综上，a取值范围为：a＞-1．
| 1 |
| 2 |
f′(x)=2x+a-
| 1 |
| 2x |
| 4x2+2ax-1 |
| 2x |
f′(x)=0⇒x1=
-a-
| ||
| 4 |
-a+
| ||
| 4 |
f'（x）＜0⇒x∈（0，x2）减函数，f'（x）＞0⇒x∈（x2，+∞）增函数，
∴x2=
-a+
| ||
| 4 |
（2）x＞0，由f（x）＞0得|x+a|＞
| lnx |
| 2x |
当0＜x＜1，
| lnx |
| 2x |
当x=1，|1+a|＞0得a≠-1，
当x＞1，不等比等价于a＜-x-
| lnx |
| 2x |
| lnx |
| 2x |
令g(x)=-x-
| lnx |
| 2x |
| 1-lnx |
| 2x2 |
| -2x2-1+lnx |
| 2x2 |
令φ（x）=-2x2-1+lnx，
φ′(x)=-4x+
| 1 |
| x |
| 1-4x2 |
| x |
φ（x）在（1，+∞）减函数，φ（x）＜φ（1）=-3＜0，
得g（x）在（1，+∞）减函数，g（x）∈（-∞，-1），
∴a＜-x-
| lnx |
| 2x |
又令h(x)=-x+
| lnx |
| 2x |
∴h′(x)=-1+
| 1-lnx |
| 2x2 |
| -2x2+1-lnx |
| 2x2 |
令ψ（x）=-2x2+1-lnx在（1，+∞）减函数，ψ（x）＜ψ（1）=-1＜0，
得h（x）在（1，+∞）是减函数，h（x）＜h（1）=-1，得a≥-1．
综上，a取值范围为：a＞-1．
点评：本题考察了函数的最值问题，函数的单调性，求参数的范围，渗透了分类讨论思想，是一道中档题．
练习册系列答案
相关题目
设f（x）在（0，+∞）上是单调递增函数，当n∈N*时，f（n）∈N*，且f[f（n）]=2n+1，则（ ）
| A、f（4）=6 |
| B、f（4）=4 |
| C、f（4）=5 |
| D、f（4）=7 |
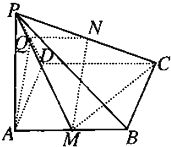已知PA⊥平面ABCD，四边形ABCD为矩形，PA=AD，M、N分别是AB、PC的中点，求证：
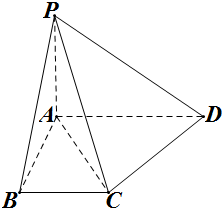如图，直角梯形ABCD中，∠ABC=∠BAD=90°，
正三棱柱ABC-A1B1C1中，BC=2，AA1=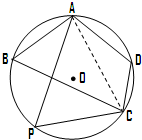
市某棚户区改造建筑用地平面示意图如图所示．经规划调研确定，棚改规划建筑用地区域是半径为R的圆面．该圆面的内接四边形ABCD是原棚户建筑用地，测量可知边界AB=AD=4万米，BC=6万米，CD=2万米．