题目内容
等差数列{an}中,a16+a17+a18=a9=-36,Sn为其前n项和.
(1)求Sn的最小值,指出Sn取最小时的n值
(2)数列bn=
,求数列{bnbn+1}的前n项和.
(1)求Sn的最小值,指出Sn取最小时的n值
(2)数列bn=
| 3 |
| an+66 |
考点:数列的求和,数列的函数特性
专题:等差数列与等比数列
分析:(1)由已知条件得a9=-36,a17=-12,从而求出Sn=-60n+
×3,利用配方法能求出n=20或n=21时,Sn最小值为S20=S21=-630.
(2)bn=
=
,bnbn+1=
-
=
-
,由此利用裂项求和法能求出数列{bnbn+1}的前n项和.
| n(n-1) |
| 2 |
(2)bn=
| 3 |
| an+66 |
| 1 |
| n+1 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
解答:
解:(1)由a16+a17+a18=a9=-36,
得a9=-36,a17=-12,
∴d=
=3.
首项a1=a9-8d=-60,an=3n-63.…(2分)
Sn=-60n+
×3
=
(n-
)2-
×
,n∈N*,…(4分)
∴n=20或n=21时,Sn最小,最小值为S20=S21=-630.…(6分)
(2)bn=
=
,
bnbn+1=
-
=
-
,…(10分)
设数列{bnbn+1}的前n项和为Tn.
则Tn=
-
+
-
+…+
-
=
-
=
.…(12分)
得a9=-36,a17=-12,
∴d=
| a17-a9 |
| 17-9 |
首项a1=a9-8d=-60,an=3n-63.…(2分)
Sn=-60n+
| n(n-1) |
| 2 |
=
| 3 |
| 2 |
| 41 |
| 2 |
| 3 |
| 2 |
| 412 |
| 2 |
∴n=20或n=21时,Sn最小,最小值为S20=S21=-630.…(6分)
(2)bn=
| 3 |
| an+66 |
| 1 |
| n+1 |
bnbn+1=
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
设数列{bnbn+1}的前n项和为Tn.
则Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n+1 |
| 1 |
| n+2 |
=
| 1 |
| 2 |
| 1 |
| n+2 |
=
| n |
| 2n+4 |
点评:本题考查数列的前n项和的求法,是中档题,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
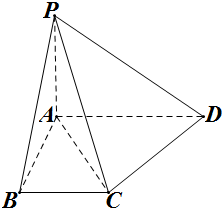 如图,直角梯形ABCD中,∠ABC=∠BAD=90°,
如图,直角梯形ABCD中,∠ABC=∠BAD=90°, 正三棱柱ABC-A1B1C1中,BC=2,AA1=
正三棱柱ABC-A1B1C1中,BC=2,AA1=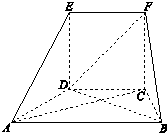 在如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,AB∥CD,AC=
在如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,AB∥CD,AC=