题目内容
已知点P是抛物线y2=4x上一点，设点P到直线x=-1的距离为d1，到直线x+2y+10=0的距离为d2，则d1+d2的最小值是（ ）
| A、5 | ||||
| B、4 | ||||
C、
| ||||
D、
|
考点：直线与圆锥曲线的关系,点到直线的距离公式
专题：圆锥曲线中的最值与范围问题
分析：如图点P到准线的距离等于点P到焦点F的距离，过焦点F作直线x+2y+10=0的垂线，此时d1+d2最小，根据抛物线方程求得F，进而利用点到直线的距离公式求得d1+d2的最小值．
解答：
解：如图，点P到准线的距离等于点P到焦点F的距离，
过焦点F作直线x+2y+10=0的垂线，
此时d1+d2最小，
∵F（1，0），
∴d1+d2=
=
．
故选：C．
过焦点F作直线x+2y+10=0的垂线，
此时d1+d2最小，
∵F（1，0），
∴d1+d2=
| |1+10| | ||
|
11
| ||
| 5 |
故选：C．
点评：本题主要考查了抛物线的简单性质，两点距离公式的应用．解此类题设宜先画出图象，进而利用数形结合的思想解决问题．
练习册系列答案
相关题目
在等差数列{an}中，a1+a9=10，则a2+a8的值为（ ）
| A、5 | B、6 | C、8 | D、10 |
设f（x）在（0，+∞）上是单调递增函数，当n∈N*时，f（n）∈N*，且f[f（n）]=2n+1，则（ ）
| A、f（4）=6 |
| B、f（4）=4 |
| C、f（4）=5 |
| D、f（4）=7 |
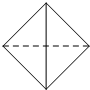
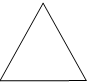
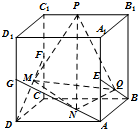已知点E、F、G分别是正方体ABCD-A1B1C1D1的棱AA1、CC1、DD1的中点，点M、N、Q、P分别在线段DF、AG、BE、C1B1上．以M、N、Q、P为顶点的三棱锥P-MNQ的俯视图不可能是（ ）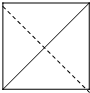
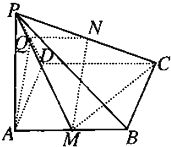已知PA⊥平面ABCD，四边形ABCD为矩形，PA=AD，M、N分别是AB、PC的中点，求证：
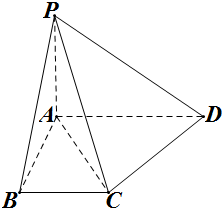如图，直角梯形ABCD中，∠ABC=∠BAD=90°，