题目内容
已知
=(l+2,0,2l),
=(6,2m-1,2),若
∥
,则l与m的值分别为( )
| a |
| b |
| a |
| b |
A、
| ||||
| B、5,2 | ||||
C、-
| ||||
| D、-5,-2 |
考点:向量的数量积判断向量的共线与垂直
专题:空间向量及应用
分析:利用向量共线定理即可得出.
解答:
解:∵
∥
,
可设
=k
,
∴
,
解得
故选:A.
| a |
| b |
可设
| a |
| b |
∴
|
解得
|
故选:A.
点评:本题考查了向量共线定理,属于基础题.

练习册系列答案
相关题目
函数f(x)=2x+3x-6的零点所在的区间是( )
| A、(0,1) |
| B、(1,2 ) |
| C、(2,3) |
| D、(3,4) |
设a>b>0,则下列不等式成立的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
函数f(x)=3sin(2x-
)的图象为M,下列结论中正确的是( )
| π |
| 3 |
A、图象M关于直线x=
| ||||
B、图象M关于点(-
| ||||
C、f(x)在区间(-
| ||||
D、由y=3sin2x的图象向右平移
|
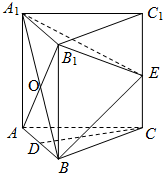 如图,在三棱柱ABC-A1B1C1中,每个侧面均为正方形,D为底边AB的中点,E为侧棱CC1的中点.
如图,在三棱柱ABC-A1B1C1中,每个侧面均为正方形,D为底边AB的中点,E为侧棱CC1的中点.