题目内容
16.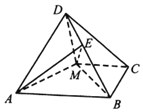 如图,四棱锥D-ABCM中,AD=DM,且AD⊥DM,底面四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,平面AMD⊥平面ABCM.
如图,四棱锥D-ABCM中,AD=DM,且AD⊥DM,底面四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,平面AMD⊥平面ABCM.(Ⅰ)求证:AD⊥BD
(Ⅱ)若点E是线段DB上的一动点,问点E在何位置时,四棱锥M-ADE的体积为$\frac{4\sqrt{2}}{9}$?
分析 (Ⅰ)推导出AM⊥BM,从而BM⊥平面DAM,由此能证明AD⊥BD.
(Ⅱ)由BM⊥平面ADM,BM=2$\sqrt{2}$,由VM-ADE=VE-ADM,能求出E为BD的三等分点时,四棱锥M-ADE的体积为$\frac{4\sqrt{2}}{9}$.
解答 证明:(Ⅰ)∵四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,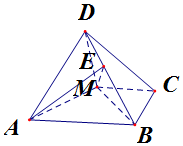
AB=2BC=2MC=4,
∴BM=AM=2$\sqrt{2}$,
∴BM2+AM2=AB2,即AM⊥BM,
∵平面ADM⊥平面ABCM,平面ADM∩平面ABCM=AM,
BM?平面ABCM,
∴BM⊥平面DAM,又DA?平面DAM,
∴AD⊥BD.
解:(Ⅱ)由(Ⅰ)知BM⊥平面ADM,BM=2$\sqrt{2}$,
设$\frac{DE}{BD}=λ$,则E到平面ADM的距离d=2$\sqrt{2}$λ,
∵△ADM是等腰直角三角形,AD⊥DM,AM=2$\sqrt{2}$,
∴AD=DM=2,
∴VM-ADE=VE-ADM=$\frac{1}{3}{S}_{△AMD}•d$=$\frac{4\sqrt{2}}{9}$,
即$\frac{1}{3}×\frac{1}{2}×2×2×2\sqrt{2}λ=\frac{4\sqrt{2}}{9}$,
解得$λ=\frac{1}{3}$,
∴E为BD的三等分点.
点评 本题考查线线垂直的证明,考查满足条件的点的位置的确定及求法,考查推理论证能力、运算求解能力、空间想象能力,考查数形结合思想、化归与转化思想,是中档题.

练习册系列答案
相关题目
14.已知φ∈($\frac{π}{2}$,π),且sinφ=$\frac{3}{5}$,若函数f(x)=sin(ωx+φ)(ω>0)的图象的相邻两条对称轴之间的距离等于$\frac{π}{2}$,则f($\frac{π}{4}$)的值为( )
| A. | -$\frac{3}{5}$ | B. | -$\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
11.《九章算术》商功章有云:今有圆困,高一丈三尺三寸、少半寸,容米二千斛,问周几何?即一圆柱形谷仓,高1丈3尺$3\frac{1}{3}$寸,容纳米2000斛(1丈=10尺,1尺=10寸,斛为容积单位,1斛≈1.62立方尺,π≈3),则圆柱底面圆的周长约为( )
| A. | 1丈3尺 | B. | 5丈4尺 | C. | 9丈2尺 | D. | 48 |
1.函数f(x)=2sin(2x+$\frac{π}{3}$+φ)(|φ|<$\frac{π}{2}$)的图象向左平移$\frac{π}{2}$个单位后关于y轴对称,则以下判断不正确的是( )
| A. | $f({x+\frac{π}{4}})$是奇函数 | B. | $({\frac{π}{4},0})$为f(x)的一个对称中心 | ||
| C. | f(x)在$({-\frac{3π}{4},-\frac{π}{4}})$上单调递增 | D. | f(x)在(0,$\frac{π}{2}$)上单调递减 |
8.若集合A={-1,2},B={0,1},则集合{z|z=x+y,x∈A,y∈B}的子集共有( )
| A. | 2个 | B. | 4个 | C. | 8个 | D. | 16个 |
5.已知数列{an}为等差数列,若a12+a102≤25恒成立,则a1+3a7的取值范围为( )
| A. | [-5,5] | B. | [-5$\sqrt{2}$,5$\sqrt{2}$] | C. | [-10,10] | D. | [-10$\sqrt{2}$,10$\sqrt{2}$] |
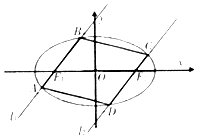 如图,过椭圆C:$\frac{{x}^{2}}{4}$+y2=1的左右焦点F1,F2分别作直线l1,l2交椭圆于A,B与C,D,且l1∥l2.
如图,过椭圆C:$\frac{{x}^{2}}{4}$+y2=1的左右焦点F1,F2分别作直线l1,l2交椭圆于A,B与C,D,且l1∥l2.