题目内容
14.已知φ∈($\frac{π}{2}$,π),且sinφ=$\frac{3}{5}$,若函数f(x)=sin(ωx+φ)(ω>0)的图象的相邻两条对称轴之间的距离等于$\frac{π}{2}$,则f($\frac{π}{4}$)的值为( )| A. | -$\frac{3}{5}$ | B. | -$\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
分析 由周期求出ω,由条件求出cosφ的值,从而求得f($\frac{π}{4}$)的值.
解答 解:根据函数f(x)=sin(ωx+φ)(ω>0)的图象的相邻两条对称轴之间的距离等于$\frac{π}{2}$,
可得$\frac{π}{ω}$=$\frac{π}{2}$,∴ω=2.
由φ∈($\frac{π}{2}$,π),且sinφ=$\frac{3}{5}$,可得 cosφ=-$\frac{4}{5}$,
∴f($\frac{π}{4}$)=sin($\frac{π}{2}$+φ)=cosφ=-$\frac{4}{5}$,
故选:B.
点评 本题主要考查正弦函数的周期性,同角三角函数的基本关系,属于基础题.

练习册系列答案
相关题目
4.设等差数列{an}满足sina4cosa7-cosa4sina7=1,公差d∈(-1,0),当且仅当n=9时,数列{an}的前n项和Sn取得最大值,求该数列首项a1的取值范围( )
| A. | $(\frac{7π}{6},\frac{4π}{3})$ | B. | $[{\frac{7π}{6},\frac{4π}{3}}]$ | C. | $(\frac{4π}{3},\frac{3π}{2})$ | D. | $[{\frac{4π}{3},\frac{3π}{2}}]$ |
5.已知数列{an}中,a1=2,an+1=an+n(n∈N+),则a4的值为( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
2.△ABC的内角A,B,C所对的边分别为a,b,c.且a:b:c=3:5:7试判断该三角形的形状( )
| A. | 钝角三角形 | B. | 锐角三角形 | C. | 直角三角形 | D. | 等边三角形 |
19.对[25,55]岁的人群随机抽取n人进行了生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图.
(Ⅰ)补全频率分布直方图并求n、a、p的值;
(Ⅱ)从年龄段在[40,50)的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在[40,45)岁的概率.

| 组数 | 分组 | 低碳族的人数 | 占本组的频率 |
| 第一组 | [25,30﹚ | 120 | 0.6 |
| 第二组 | [30,35﹚ | 195 | p |
| 第三组 | [35,40﹚ | 100 | 0.5 |
| 第四组 | [40,45﹚ | a | 0.4 |
| 第五组 | [45,50﹚ | 30 | 0.3 |
| 第六组 | [50,55] | 15 | 0.3 |
(Ⅱ)从年龄段在[40,50)的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在[40,45)岁的概率.
6.设函数f(x)=sin(2x+$\frac{π}{6}$)+$\sqrt{3}$cos(2x+$\frac{π}{6}$),则( )
| A. | y=f(x)在(0,$\frac{π}{2}$)单调递增,其图象关于直线x=$\frac{π}{4}$对称 | |
| B. | y=f(x)在(0,$\frac{π}{2}$)单调递增,其图象关于直线x=$\frac{π}{2}$对称 | |
| C. | y=f(x)在(0,$\frac{π}{2}$)单调递减,其图象关于直线x=$\frac{π}{4}$对称 | |
| D. | y=f(x)在(0,$\frac{π}{2}$)单调递减,其图象关于直线x=$\frac{π}{2}$对称 |
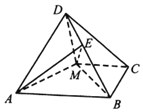 如图,四棱锥D-ABCM中,AD=DM,且AD⊥DM,底面四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,平面AMD⊥平面ABCM.
如图,四棱锥D-ABCM中,AD=DM,且AD⊥DM,底面四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,平面AMD⊥平面ABCM.