题目内容
11.《九章算术》商功章有云:今有圆困,高一丈三尺三寸、少半寸,容米二千斛,问周几何?即一圆柱形谷仓,高1丈3尺$3\frac{1}{3}$寸,容纳米2000斛(1丈=10尺,1尺=10寸,斛为容积单位,1斛≈1.62立方尺,π≈3),则圆柱底面圆的周长约为( )| A. | 1丈3尺 | B. | 5丈4尺 | C. | 9丈2尺 | D. | 48 |
分析 首先根据圆柱的体积公式:V=Sh,求得圆柱的底面积S,然后根据面积S=πr2,求得半径,进而即可求得周长.
解答 解:由题意得:2000×1.62=S(10+3+$\frac{10}{3}$×$\frac{1}{10}$),
解得S=$\frac{2000×1.62}{\frac{40}{3}}$=243,
因为S=πr2,
所以,r=9,
所以,周长=2πr=2×3×9=54(尺),
54尺=5丈4尺,
故选:B.
点评 本题考查了圆柱的体积公式在实际中的应用,关键是熟记公式.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
10.已知P是边长为4的正△ABC的边BC上的动点,则$\overrightarrow{AP}•(\overrightarrow{AB}+\overrightarrow{AC})$( )
| A. | 最大值为16 | B. | 是定值24 | C. | 最小值为4 | D. | 是定值4 |
7.如果圆柱的轴截面的周长l为定值,则圆柱体积的最大值为( )
| A. | ($\frac{l}{6}$)3π | B. | ($\frac{l}{3}$)3π | C. | ($\frac{l}{4}$)3π | D. | $\frac{1}{4}$($\frac{l}{4}$)3π |
1.定义“函数y=f(x)是D上的a级类周期函数”如下:函数y=f(x),x∈D,对于给定的非零常数 a,总存在非零常数T,使得定义域D内的任意实数x都有af(x)=f(x+T)恒成立,此时T为f(x)的周期.若y=f(x)是[1,+∞)上的a级类周期函数,且T=1,当x∈[1,2)时,f(x)=2x+1,且y=f(x)是[1,+∞)上的单调递增函数,则实数a的取值范围为( )
| A. | $[{\frac{5}{6},+∞})$ | B. | [2,+∞) | C. | $[{\frac{5}{3},+∞})$ | D. | [10,+∞) |
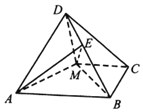 如图,四棱锥D-ABCM中,AD=DM,且AD⊥DM,底面四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,平面AMD⊥平面ABCM.
如图,四棱锥D-ABCM中,AD=DM,且AD⊥DM,底面四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,平面AMD⊥平面ABCM.