题目内容
已知数列{2nan}的前n项和Sn=9-6n
(1)求数列{an}的通项公式;
(2)求数列{Tn}的前n项和Tn.
(1)求数列{an}的通项公式;
(2)求数列{Tn}的前n项和Tn.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)在已知的数列递推式中分别取n=1和n≥2求解数列的通项公式,验证首项后得答案;
(2)利用等比数列的前n项和求数列{an}的前n项和.
(2)利用等比数列的前n项和求数列{an}的前n项和.
解答:
解:(1)当n=1时,2a1=3,a1=
,
当n≥2时,2nan=Sn-Sn-1=9-6n-[9-6(n-1)]=-6,
∴an=
,
验证n=1时上式不成立,
∴an=
;
(2)Tn=a1+a2+…+an=
+(-
)+(-
)+…+(-
)
=
-6×
=
-
.
| 3 |
| 2 |
当n≥2时,2nan=Sn-Sn-1=9-6n-[9-6(n-1)]=-6,
∴an=
| -6 |
| 2n |
验证n=1时上式不成立,
∴an=
|
(2)Tn=a1+a2+…+an=
| 3 |
| 2 |
| 6 |
| 22 |
| 6 |
| 23 |
| 6 |
| 2n |
=
| 3 |
| 2 |
| ||||
1-
|
| 3 |
| 2n-1 |
| 3 |
| 2 |
点评:本题考查了由数列前n项和求数列的通项公式,考查了等比数列的前n项和,是中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
函数y=
sinx+cosx(x∈[0,π])的值域是( )
| 3 |
| A、[-2,2] | ||
| B、[-1,2] | ||
| C、[-1,1] | ||
D、[-
|
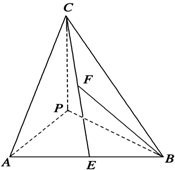 如图,四面体P-ABC中,PA、PB、PC两两垂直,PA=PB=2,PC=4,E是AB的中点,F是CE的中点.
如图,四面体P-ABC中,PA、PB、PC两两垂直,PA=PB=2,PC=4,E是AB的中点,F是CE的中点.