题目内容
函数f（x）=tan2（x+
）的单调递增区间为 ．
| π |
| 4 |
考点：两角和与差的正切函数
专题：三角函数的图像与性质
分析：令kπ≤x+
＜kπ+
，k∈z，求得x的范围，可得函数的增区间．
| π |
| 4 |
| π |
| 2 |
解答：
解：令kπ≤x+
＜kπ+
，k∈z，求得 kπ-
≤x＜kπ+
，
可得函数的增区间为[kπ-
，kπ+
），k∈z，
故答案为：[kπ-
，kπ+
），k∈z．
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
可得函数的增区间为[kπ-
| π |
| 4 |
| π |
| 4 |
故答案为：[kπ-
| π |
| 4 |
| π |
| 4 |
点评：本题主要正切函数的图象和性质，得到kπ≤x+
＜kπ+
，k∈z，是解题的关键，属于中档题．
| π |
| 4 |
| π |
| 2 |
练习册系列答案
优百分课时互动系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
相关题目
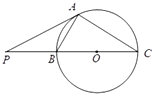如图，PA是圆O的切线，切点为A，PO交圆O于B，C两点，PA=