题目内容
19.函数f(x)=cosx+|cosx|,x∈R是( )| A. | 最小正周期是π | B. | 区间[0,2]上的增函数 | ||
| C. | 图象关于点(kπ,0)(k∈Z)对称 | D. | 周期函数且图象有无数条对称轴 |
分析 化简函数f(x),根据函数的图象与性质判断四个选项是否正确即可.
解答 解:函数f(x)=cosx+|cosx|
=$\left\{\begin{array}{l}{2cosx,x∈[-\frac{π}{2}+2kπ,\frac{π}{2}+2kπ],k∈Z}\\{0,x∈(\frac{π}{2}+2kπ,\frac{π}{2}+\frac{3π}{2}+2kπ),k∈Z}\end{array}\right.$,
∴f(x)是周期函数,且最小正周期为2π,A错误;
∵2>$\frac{π}{2}$,∴x∈[0,2]时,f(x)不是增函数,B错误;
f(x)的图象不关于点(kπ,0)(k∈Z)对称,C错误;
f(x)是周期函数且图象有无数条对称轴为x=kπ,k∈Z,D正确.
故选:D.
点评 本题考查了余弦函数的图象与性质的应用问题,是基础题.

练习册系列答案
相关题目
7.若随机变量X服从正态分布N(1,4),设P(0<X<3)=m,P(-1<X<2)=n,则m、n的大小关系为( )
| A. | m>n | B. | m<n | C. | m=n | D. | 不确定 |
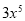 +
+ -8x+5在x=2时的值。
-8x+5在x=2时的值。