题目内容
已知函数f(x)=sinx(2cos2
-1)+cosx•sinθ(0<θ<π)在x=π处取最小值.
(1)求θ的值;
(2)若f(2x-
)=
,且x∈(
π,π),求sin2x的值.
| θ |
| 2 |
(1)求θ的值;
(2)若f(2x-
| π |
| 3 |
| 1 |
| 3 |
| 3 |
| 4 |
考点:三角函数中的恒等变换应用,二倍角的正弦
专题:三角函数的求值
分析:(1)化简得f(x)=sin(x+θ)从而可求θ的值;
(2)若f(2x-
)=
,且x∈(
π,π),可先求f(2x-
)=cos(2x-
)=
,sin(2x-
)=-
=
从而可求sin2x的值.
(2)若f(2x-
| π |
| 3 |
| 1 |
| 3 |
| 3 |
| 4 |
| π |
| 3 |
| π |
| 3 |
| 1 |
| 3 |
| π |
| 3 |
1-
|
| -2 |
| 3 |
| 2 |
解答:
解:(1)f(x)=sinxcosθ+cosx•sinθ=sin(x+θ)
∴π+θ=-
+2kπ⇒θ=-
π+2kπ,
∴θ=
(2)f(x)=sin(x+
)=cosx
∴f(2x-
)=cos(2x-
)=
由
π<x<π⇒
π<2x<2π⇒
π-
<2x-
<2π-
∴sin(2x-
)=-
=
∴sin2x=sin[(2x-
)+
]=
sin(2x-
)+
cos(2x-
)=
•
+
•
=
+
∴π+θ=-
| π |
| 2 |
| 3 |
| 2 |
∴θ=
| π |
| 2 |
(2)f(x)=sin(x+
| π |
| 2 |
∴f(2x-
| π |
| 3 |
| π |
| 3 |
| 1 |
| 3 |
由
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
∴sin(2x-
| π |
| 3 |
1-
|
| -2 |
| 3 |
| 2 |
∴sin2x=sin[(2x-
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| ||
| 2 |
| π |
| 3 |
| -1 |
| 2 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
| 1 |
| 3 |
-
| ||
| 3 |
| ||
| 6 |
点评:本题主要考察三角函数中的恒等变换应用和二倍角的正弦公式的应用,属于中档题.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
下列命题中正确的是( )
A、“m=
| ||
| B、“直线l垂直平面α内无数条直线”是“直线l垂直于平面α”的充分条件 | ||
| C、已知a,b,c为非零向量,则“a•b=a•c”是“b=c”的充要条件 | ||
| D、p:存在x∈R,x2+2x+2≤0,则¬p:任意x∈R,x2+2x+2>0. |
分式方程
+1=
的解是( )
| x-3 |
| x-2 |
| 3 |
| 2-x |
| A、2 | B、1 | C、-1 | D、-2 |
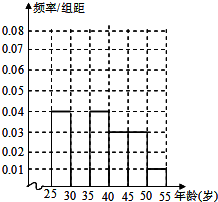 某高中社团进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次是否开通“微博”的调查,若开通“微博”的称为“时尚族”,否则称为“非时尚族”.通过调查分别得到如图所示统计表,如图2所示各年龄段人数频率分布直方图.
某高中社团进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次是否开通“微博”的调查,若开通“微博”的称为“时尚族”,否则称为“非时尚族”.通过调查分别得到如图所示统计表,如图2所示各年龄段人数频率分布直方图. 已知⊙C:x2+(y-1)2=1和直线l:y=-1,由⊙C外一点P(a,b)向⊙C引切线PQ,切点为Q,且满足PQ等于P到直线l的距离.
已知⊙C:x2+(y-1)2=1和直线l:y=-1,由⊙C外一点P(a,b)向⊙C引切线PQ,切点为Q,且满足PQ等于P到直线l的距离.