题目内容
已知12＜a＜60，10＜b＜20，则
的取值范围是 ．
| b |
| a |
考点：简单线性规划
专题：不等式的解法及应用
分析：直接由已知条件作出关于a，b的可行域，然后由
的几何意义得答案．
| b |
| a |
解答：
解：由12＜a＜60，10＜b＜20作出可行域如图，
的几何意义为可行域内的动点与原点连线的斜率，
kOA=
，kOB=
．
∴
的取值范围是(
，
)．
故答案为：(
，
)．
| b |
| a |
kOA=
| 1 |
| 6 |
| 5 |
| 3 |
∴
| b |
| a |
| 1 |
| 6 |
| 5 |
| 3 |
故答案为：(
| 1 |
| 6 |
| 5 |
| 3 |
点评：本题考查了简单的线性规划，考查了数形结合的解题思想方法，是中档题．
练习册系列答案
相关题目
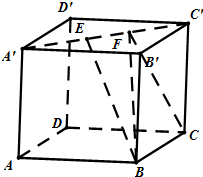如图，正方体ABCD-A′B′C′D′的棱线长为1，线段AC′上有两个动点E，F，且EF=
| ||
| 2 |
①直线AA′与CF是异面直线
②三棱锥B′BEF体积为定值
③异面直线DD′与BE所成角的余弦值范围是[
| ||
| 2 |
| ||
| 3 |
④BD⊥EF．
| A、①②④ | B、②④ |
| C、②③ | D、②③④ |
下列写法中正确的是（ ）
| A、∅={∅} | B、∅⊆{0} |
| C、∅={0} | D、0∈∅ |