题目内容
合肥一中每年五月举行校园微型博览会,在会馆入口处准备了A,B,C三种形式的校长签名纪念卡片供参观同学抽取.
(Ⅰ)若有大量纪念卡,其中20%的A卡,现抽取了5张,求其中A卡的张数X的分布列及其数学期望E(X);(注:在总体数量特别大时,无放回抽样可以近似看作有放回抽样)
(Ⅱ)活动结束,剩余若干纪念卡,从中任意抽取1张纪念卡,得到A卡的概率是
,任意抽取2张卡,没有B卡的概率是
,求证:任意抽取2张卡,至少得到1张A卡的概率不大于
,并指出余下的卡中哪种卡最少.
(Ⅰ)若有大量纪念卡,其中20%的A卡,现抽取了5张,求其中A卡的张数X的分布列及其数学期望E(X);(注:在总体数量特别大时,无放回抽样可以近似看作有放回抽样)
(Ⅱ)活动结束,剩余若干纪念卡,从中任意抽取1张纪念卡,得到A卡的概率是
| 3 |
| 7 |
| 1 |
| 4 |
| 5 |
| 7 |
考点:离散型随机变量的期望与方差,相互独立事件的概率乘法公式
专题:应用题,概率与统计
分析:(Ⅰ)抽取的5张中A卡的张数X~B(5,0.2),可求A卡的张数X的分布列及其数学期望E(X);
(Ⅱ)假设其余n张卡,A卡有m张,则2m<n,即2m≤n-1,任取2张卡,至少得到1张A卡的概率P=
+
•
,即可证明结论;求出任意抽取2张卡,至少得到1张B卡的概率,即可得出结论.
(Ⅱ)假设其余n张卡,A卡有m张,则2m<n,即2m≤n-1,任取2张卡,至少得到1张A卡的概率P=
| 3 |
| 7 |
| 4 |
| 7 |
| m-1 |
| n-1 |
解答:
(Ⅰ)解:抽取的5张中A卡的张数X~B(5,0.2),分布列为
E(X)=5×0.2=1;
(Ⅱ)证明:假设其余n张卡,A卡有m张,则2m<n,即2m≤n-1.
任取2张卡,至少得到1张A卡的概率P=
+
•
,
∵
<
≤
,
∴P<
;
由于任意抽取2张卡,至少得到1张B卡的概率是1-
=
>
,
∴B卡多于A卡,超过
,
∴C卡所占比例少于1-
-
=
,
∴C卡最少.
| X | 0 | 1 | 2 | 3 | 4 | 5 | ||||||||||
| P |
|
|
|
|
|
0.25 |
(Ⅱ)证明:假设其余n张卡,A卡有m张,则2m<n,即2m≤n-1.
任取2张卡,至少得到1张A卡的概率P=
| 3 |
| 7 |
| 4 |
| 7 |
| m-1 |
| n-1 |
∵
| m-1 |
| n-1 |
| m |
| n-1 |
| 1 |
| 2 |
∴P<
| 5 |
| 7 |
由于任意抽取2张卡,至少得到1张B卡的概率是1-
| 1 |
| 4 |
| 3 |
| 4 |
| 5 |
| 7 |
∴B卡多于A卡,超过
| 3 |
| 7 |
∴C卡所占比例少于1-
| 3 |
| 7 |
| 3 |
| 7 |
| 1 |
| 7 |
∴C卡最少.
点评:本题考查离散型随机变量的分布列及其数学期望,考查概率的计算,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
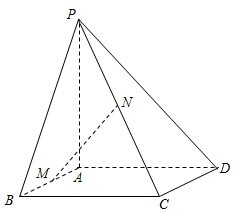 如图,在四棱锥中,底面ABCD为矩形,PA⊥底面ABCD,M、N分别是AB、PC中点.
如图,在四棱锥中,底面ABCD为矩形,PA⊥底面ABCD,M、N分别是AB、PC中点.