题目内容
已知圆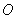 的方程为
的方程为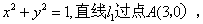 且与圆
且与圆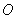 相切.
相切.
(Ⅰ)求直线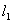 的方程;
的方程;
(Ⅱ)设圆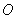 与
与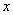 轴交于
轴交于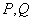 两点,M是圆
两点,M是圆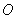 上异于
上异于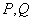 的任意一点,过点
的任意一点,过点 且与
且与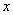 轴垂直的直线为
轴垂直的直线为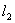 ,直线
,直线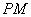 交直线
交直线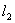 于点
于点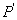 ,直线
,直线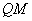 交直线
交直线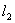 于点
于点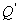 .
.
求证:以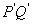 为直径的圆
为直径的圆 总过定点,并求出定点坐标.
总过定点,并求出定点坐标.
解:(Ⅰ)∵直线 过点
过点 ,且与圆
,且与圆 :
: 相切,
相切,
设直线 的方程为
的方程为 ,即
,即 ,
,
则圆心 到直线
到直线 的距离为
的距离为 ,解得
,解得 ,
,
∴直线 的方程为
的方程为 ,即
,即 .
.
(Ⅱ)对于圆方程 ,令
,令 ,得
,得 ,即
,即 .又直线
.又直线 过点
过点 且与
且与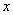 轴垂直,∴直线
轴垂直,∴直线 方程为
方程为 ,设
,设 ,则直线
,则直线 方程为
方程为
解方程组 ,得
,得 同理可得,
同理可得,
∴以 为直径的圆
为直径的圆 的方程为,
的方程为,
又 ,∴整理得
,∴整理得 ,
,
若圆 经过定点,只需令
经过定点,只需令 ,从而有
,从而有 ,解得
,解得 ,
,
∴圆 总经过定点坐标为
总经过定点坐标为 .
.

练习册系列答案
相关题目
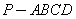 中,
中,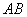 //
//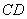 ,
,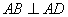 ,
,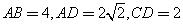 ,
,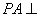 平面
平面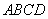 ,
,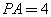 .
. 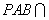 平面
平面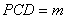 ,求证:
,求证: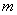 ;
;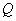 为线段
为线段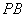 上一点,且直线
上一点,且直线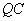 与平面
与平面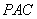 所成角的正弦值为
所成角的正弦值为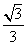 ,求
,求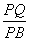 的值.
的值.
 与直线
与直线 围成的封闭图形的面积?
围成的封闭图形的面积?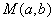 ,且满足
,且满足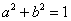 ,已知圆
,已知圆 ,
,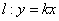 ,下列四个命题:
,下列四个命题: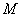 和任意实数
和任意实数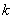 ,直线
,直线 和圆
和圆 +
+ +
+ =
= ,则△PAB的面积与△ABC的面积比为( )
,则△PAB的面积与△ABC的面积比为( ) 2:3
2:3  1:3
1:3  1:4
1:4  1:6
1:6 的定义域为
的定义域为 ,
, 且对于任意的
且对于任意的 都有
都有 ,若在区间
,若在区间 上函数
上函数 恰有四个不同零点,则实数
恰有四个不同零点,则实数 的取值范围为( )
的取值范围为( )



