题目内容
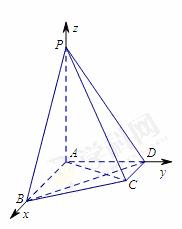
在四棱锥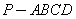 中,
中,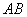 //
//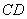 ,
,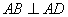 ,
,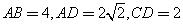 ,
,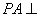 平面
平面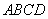 ,
,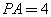 .
.
(Ⅰ)设平面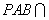 平面
平面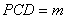 ,求证:
,求证: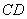 //
//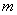 ;
;
(Ⅱ)设点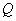 为线段
为线段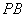 上一点,且直线
上一点,且直线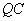 与平面
与平面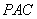 所成角的正弦值为
所成角的正弦值为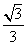 ,求
,求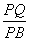 的值.
的值.

解:(Ⅰ)因为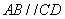 ,
,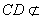 平面
平面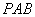 ,
,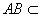 平面
平面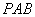 ,
,
所以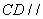 平面
平面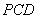 ,平面
,平面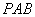
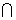 平面
平面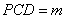 ,
,
所以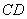 //
//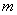
(Ⅱ)
法一:因为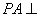 平面
平面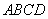 ,
,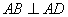 ,所以如图建立直角坐标系,则
,所以如图建立直角坐标系,则
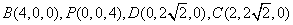
 所以
所以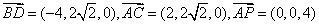 ,
,
所以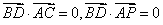 ,所以面
,所以面 的法向量为
的法向量为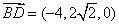
设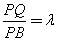 (其
(其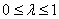 ),
),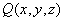 ,
,
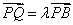 ,所以
,所以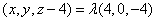
所以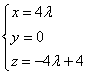 ,即
,即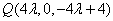 ,
,
所以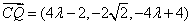
因为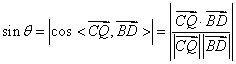
代入得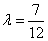
所以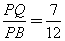
法二:因为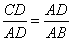 ,所以
,所以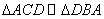 ,所以
,所以
即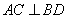
又因为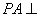 平面
平面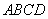 ,所以
,所以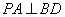 ,所以
,所以
设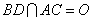 ,连接
,连接 ,过
,过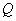 作
作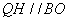 ,交
,交 于
于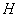 ,则
,则
连接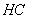 ,则
,则 即直线
即直线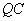 与平面
与平面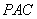 所成的角.
所成的角.
设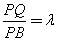 (其
(其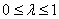 ),则
),则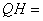
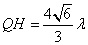
在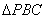 中用余弦定理知,
中用余弦定理知,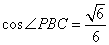
 ,在
,在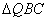 中用余弦定理知,
中用余弦定理知,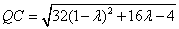 -
-
在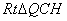 中,
中,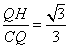
代入得得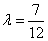
所以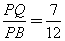

练习册系列答案
相关题目
 中,一单位圆的圆心的初始位置在
中,一单位圆的圆心的初始位置在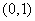 ,此时圆上一点
,此时圆上一点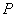 的位置在
的位置在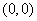 ,圆在
,圆在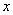 轴上沿正向滚动。当圆滚动到圆心位于
轴上沿正向滚动。当圆滚动到圆心位于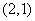 时,
时,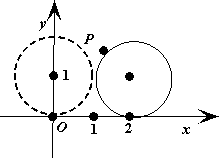

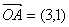 ,
,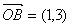 ,若
,若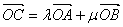 ,且
,且 ,则用阴影表示
,则用阴影表示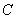 点所有可能的位置区域正确的是( )
点所有可能的位置区域正确的是( )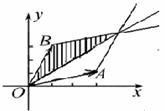

 ,则
,则 的值等于( )
的值等于( ) 的方程为
的方程为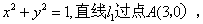 且与圆
且与圆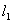 的方程;
的方程;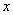 轴交于
轴交于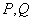 两点,M是圆
两点,M是圆 且与
且与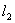 ,直线
,直线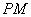 交直线
交直线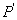 ,直线
,直线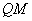 交直线
交直线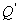 .
.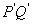 为直径的圆
为直径的圆 总过定点,并求出定点坐标.
总过定点,并求出定点坐标.