题目内容
在平面直角坐标系xOy中,不过原点的直线l与抛物线y2=4x相交于不同的A,B两点.
(1)如果直线l过抛物线的焦点,求
•
的值;
(2)如果OA⊥OB,证明直线l必过一定点,并求出该定点.
(1)如果直线l过抛物线的焦点,求
| OA |
| OB |
(2)如果OA⊥OB,证明直线l必过一定点,并求出该定点.
考点:抛物线的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)根据抛物线的方程得到焦点的坐标,设出直线与抛物线的两个交点和直线方程,是直线的方程与抛物线方程联立,得到关于y的一元二次方程,根据根与系数的关系,表达出两个向量的数量积.
(2)设出直线的方程,同抛物线方程联立,得到关于y的一元二次方程,根据根与系数的关系表示出数量积,根据数量积等于0,做出数量积表示式中的b的值,即得到定点的坐标.
(2)设出直线的方程,同抛物线方程联立,得到关于y的一元二次方程,根据根与系数的关系表示出数量积,根据数量积等于0,做出数量积表示式中的b的值,即得到定点的坐标.
解答:
解:(1)由题意:抛物线焦点为(1,0),
设l:x=ty+1代入抛物线y2=4x消去x得,
y2-4ty-4=0,设A(x1,y1),B(x2,y2),
则y1+y2=4t,y1y2=-4;
∴
•
=x1x2+y1y2=(ty1+1)(ty2+1)+y1y2
=t2y1y2+t(y1+y2)+1+y1y2
=-4t2+4t2+1-4=-3.
(2)设l:x=ty+b代入抛物线y2=4x,消去x得
y2-4ty-4b=0设A(x1,y1),B(x2,y2)
则y1+y2=4t,y1y2=-4b
∴
•
=(ty1+b)(ty2+b)+y1y2
=t2y1y2+bt(y1+y2)+b2+y1y2
=-4bt2+4bt2+b2-4b=b2-4b=0
∴b=4(0舍去).
∴直线l过定点(4,0).
设l:x=ty+1代入抛物线y2=4x消去x得,
y2-4ty-4=0,设A(x1,y1),B(x2,y2),
则y1+y2=4t,y1y2=-4;
∴
| OA |
| OB |
=t2y1y2+t(y1+y2)+1+y1y2
=-4t2+4t2+1-4=-3.
(2)设l:x=ty+b代入抛物线y2=4x,消去x得
y2-4ty-4b=0设A(x1,y1),B(x2,y2)
则y1+y2=4t,y1y2=-4b
∴
| OA |
| OB |
=t2y1y2+bt(y1+y2)+b2+y1y2
=-4bt2+4bt2+b2-4b=b2-4b=0
∴b=4(0舍去).
∴直线l过定点(4,0).
点评:本题考查了直线与抛物线相交问题转化为抛物线的方程联立得到根与系数的关系、数量积运算、直线过定点问题等基础知识与基本技能方法,属于中档题.

练习册系列答案
相关题目
定义a?b=
,则函数f(x)=x?(2-x)的值域是( )
|
| A、(-∞,1) | B、(-∞,1] |
| C、R | D、(1,+∞) |
函数f(x)=lg(2x-3)的定义域是( )
A、[
| ||
B、(-∞,
| ||
C、(
| ||
D、(-∞,
|
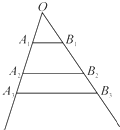 如图,互不相同的点A1,A2,…,An,…和B1,B2,…,Bn,…分别在角O的两条边上,所有AnBn相互平行,且所有梯形AnBnBn+1An+1的面积均相等.设OAn=an,若a1=1,a2=2,则a9=( )
如图,互不相同的点A1,A2,…,An,…和B1,B2,…,Bn,…分别在角O的两条边上,所有AnBn相互平行,且所有梯形AnBnBn+1An+1的面积均相等.设OAn=an,若a1=1,a2=2,则a9=( )