题目内容
下列命题:
①三角形ABC中,若a2+b2-c2-ab=0,则C=60°;
②ax(x-1)<0(a≠0)的解集是(0,1);
③Sn是数列{an}的前n项和,若Sn=n2+1,则an=2n-1;
④Sn是数列{an}的前n项和,若Sn=2n-1,则数列{an}是等比数列.
其中正确命题的序号是: .
①三角形ABC中,若a2+b2-c2-ab=0,则C=60°;
②ax(x-1)<0(a≠0)的解集是(0,1);
③Sn是数列{an}的前n项和,若Sn=n2+1,则an=2n-1;
④Sn是数列{an}的前n项和,若Sn=2n-1,则数列{an}是等比数列.
其中正确命题的序号是:
考点:命题的真假判断与应用
专题:简易逻辑
分析:由余弦定理结合已知求得C判断①;当a<0时求解不等式判断②;分别由数列的前n项和求出通项公式判断③④.
解答:
解:对于①,三角形ABC中,若a2+b2-c2-ab=0,则cosC=
=
=
,C=60°,命题①正确;
对于②,当a<0时,ax(x-1)<0(a≠0)的解集是(-∞,0)∪(1,+∞),命题②错误;
对于③,Sn是数列{an}的前n项和,若Sn=n2+1,则an=
,命题③错误;
对于④,Sn是数列{an}的前n项和,若Sn=2n-1,则an=2n-1,数列{an}是等比数列,命题④正确.
故答案为:①④.
| a2+b2-c2 |
| 2ab |
| ab |
| 2ab |
| 1 |
| 2 |
对于②,当a<0时,ax(x-1)<0(a≠0)的解集是(-∞,0)∪(1,+∞),命题②错误;
对于③,Sn是数列{an}的前n项和,若Sn=n2+1,则an=
|
对于④,Sn是数列{an}的前n项和,若Sn=2n-1,则an=2n-1,数列{an}是等比数列,命题④正确.
故答案为:①④.
点评:本题考查了命题的真假判断与应用,考查了等差数列和等比数列的判断,是中档题.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
在可行域内任取一点,如框图所示进行操作,则能输出数对(x,y)的概率是( )


A、
| ||
B、
| ||
C、
| ||
D、
|
一个袋中装有3个红球和3个白球,现从袋中取出1球,然后放回袋中再取出一球,则取出的两个球是同色球的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
方程|x+1|=2x根的个数为( )
| A、0 | B、1 | C、2 | D、3 |
已知x0是函数f(x)=(
)x+
的一个零点,若x1∈(-∞,x0),x2∈(x0,-1),则( )
| 1 |
| 2 |
| 1 |
| 1+x |
| A、f(x1)<0,f(x2)<0 |
| B、f(x1)<0,f(x2)>0 |
| C、f(x1)>0,f(x2)<0 |
| D、f(x1)>0,f(x2)>0 |
已知对任意的x,y∈R,都有f(x)+f(y)=2f(
)•f(
),f(0)≠0,则f(x)为( )
| x+y |
| 2 |
| x-y |
| 2 |
| A、是奇函数 |
| B、是偶函数 |
| C、既是奇函数又是偶函数 |
| D、无法确定f(x)奇偶性 |
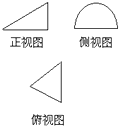 如图是某几何体的三视图,其中正视图是斜边长为2a的直角三角形,侧视图是半径为a的半圆,则该几何体的体积是( )
如图是某几何体的三视图,其中正视图是斜边长为2a的直角三角形,侧视图是半径为a的半圆,则该几何体的体积是( )A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
 如图,已知长方体ABCD-A1B1C1D1中,AB=2
如图,已知长方体ABCD-A1B1C1D1中,AB=2