题目内容
已知函数f(x)=a-
,a∈R.判断函数f(x)的奇偶性,并说明理由.
| 2 |
| 2x+1 |
考点:函数奇偶性的判断
专题:函数的性质及应用
分析:根据函数奇偶性的定义进行判断即可.
解答:
解:f(x)的定义域为R,关于原点中心对称 …(1分)
若f(x)为奇函数,则f(0)=0,即f(0)=a-1=0,解得a=1,…(3分)
此时,f(x)=1-
=
,
∴f(-x)=
=
=-
=-f(x)满足是奇函数.
当a≠1时,f(1)=a-
,f(-1)=a-
,此时f(-1)≠=f(1),
此时f(x)是非奇非偶函数.
若f(x)为奇函数,则f(0)=0,即f(0)=a-1=0,解得a=1,…(3分)
此时,f(x)=1-
| 2 |
| 2x+1 |
| 2x-1 |
| 2x+1 |
∴f(-x)=
| 2-x-1 |
| 2-x+1 |
| 1-2x |
| 1+2x |
| 2x-1 |
| 2x+1 |
当a≠1时,f(1)=a-
| 2 |
| 3 |
| 4 |
| 3 |
此时f(x)是非奇非偶函数.
点评:本题主要考查函数奇偶性的判断,根据奇偶性的定义是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
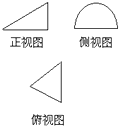 如图是某几何体的三视图,其中正视图是斜边长为2a的直角三角形,侧视图是半径为a的半圆,则该几何体的体积是( )
如图是某几何体的三视图,其中正视图是斜边长为2a的直角三角形,侧视图是半径为a的半圆,则该几何体的体积是( )A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
不等式x2-2x-3<0的解集是( )
| A、{x|x<-1} |
| B、{x|x>3} |
| C、{x|-1<x<3} |
| D、{x|x<-1或x>3} |
下列函数为偶函数的是( )
A、y=x
| ||
| B、y=sinx | ||
| C、y=cosx | ||
| D、y=x3 |
若直线y=2ax-2与y=(a+2)x+1平行,则a=( )
| A、2 | B、1 | C、-1 | D、0 |