题目内容
甲、乙、丙、丁四个人排成一行，则乙、丙相邻的排法种数是（ ）
| A、6 | B、8 | C、12 | D、24 |
考点：计数原理的应用
专题：排列组合
分析：采取分步计数原理，先乙、丙捆绑在一起看作一个符合元素，再和甲丁全排列，问题得以解决
解答：
解：把乙、丙捆绑在一起看作一个符合元素，再和甲丁全排列，故有
•
=12，
故选：C．
| A | 2 2 |
| A | 3 3 |
故选：C．
点评：本题考查了分步计数原理，相邻问题采用捆绑，属于基础题
练习册系列答案
相关题目
如图，已知长方体ABCD-A1B1C1D1中，AB=2
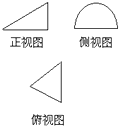如图是某几何体的三视图，其中正视图是斜边长为2a的直角三角形，侧视图是半径为a的半圆，则该几何体的体积是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
已知x、y满足条件
，则4x+2y的最小值为（ ）
|
| A、5 | B、-5 | C、12 | D、-12 |
已知函数y=f（x）是奇函数，当x≥0，f（x）=3x-1，设f（x）的反函数是y=g（x），则g（-8）=（ ）
| A、-2 | B、2 | C、-3 | D、3 |
不等式x2-2x-3＜0的解集是（ ）
| A、{x|x＜-1} |
| B、{x|x＞3} |
| C、{x|-1＜x＜3} |
| D、{x|x＜-1或x＞3} |