题目内容
16．函数y=cos2x-sin2x+sin2x的周期为π．分析 利用二倍角和辅助角公式，求得y=$\sqrt{2}$sin（2x+$\frac{π}{4}$），由正弦函数周期公式，求得周期为π．
解答 解：y=cos2x-sin2x+sin2x，
=cos2x+sin2x，
=$\sqrt{2}$sin（2x+$\frac{π}{4}$），
由正弦函数的周期T=$\frac{2π}{ω}$=π，
函数的周期为π，
故答案为：π．
点评 本题考查二倍角和辅助角公式及正弦函数周期，属于基础题．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
6．在△ABC中，sin（A+B）+2sin（B+C）cos（A+C）=0，则△ABC一定是（ ）
| A． | 等腰直角三角形 | B． | 等腰三角形 | C． | 直角三角形 | D． | 等边三角形 |
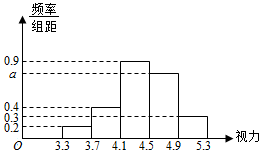某市教育主管部门为调查该市高三学生的视力情况，从全市随机抽取了100名学生迸行检测，并将视力以[3.3，3.7），[3.7，4.1），[4.1，4.5），[4.5，4.9），[4.9，5.3]分段进行统计，得到如图所示的频率分布直方图．