题目内容
8.已知函数f(x)=mx+3,g(x)=x2+2x+m.(I)解不等式f(x)≥g(x);
(Ⅱ)若不等式f(x)+g(x)≥0对任意的x∈(-1,+∞)恒成立,求实数m的取值范围.
分析 (I)整理不等式可得x2-(m-2)x+m-3≤0,利用因式分解得出两根为1和m-3,分别讨论根的大小,得出解集;
(Ⅱ)整理不等式得x2+(2+m)x+m+3≥0对任意的x∈(-1,+∞)恒成立,构造函数令h(x)=x2+(2+m)x+m+3,根据二次函数的性质分别对△
进行讨论即可得出m的范围.
解答 解:(I)f(x)≥g(x),
∴mx+3≥x2+2x+m,
∴x2-(m-2)x+m-3≤0,
∴当m-3>1即m>4时,
1≤x≤m-3,
当m-3=1时,即m=4时,
x=1,
当m-3<1即m<4时,
m-3≤x≤1;
(Ⅱ)f(x)+g(x)≥0对任意的x∈(-1,+∞)恒成立,
∴x2+(2+m)x+m+3≥0对任意的x∈(-1,+∞)恒成立,
∴令h(x)=x2+(2+m)x+m+3,
∵h(-1)=1-2-m+m+3=2>0,
当△=(m+2)2-4(m+3)≤0,即$-2\sqrt{2}$≤m≤2$\sqrt{2}$,恒成立,
当△>0时,
只需-$\frac{2+m}{2}$≤-1,
∴m≥0,
故m的范围为m≥$-2\sqrt{2}$.
点评 考查了二次不等式的解的求法和利用二次函数对△值和对称轴讨论解决恒成立问题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
18.已知$\overrightarrow{OA}$=(1,-2),$\overrightarrow{OB}$=(-3,1),则$\overrightarrow{AB}$=( )
| A. | (4,-3) | B. | (-4,3) | C. | (-2,-1) | D. | (2,1) |
19.甲、乙、丙三人站成一排站法的种数共有( )
| A. | 6 | B. | 3 | C. | 9 | D. | 12 |
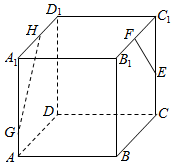 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,点E、F分别为边CC1、B1C1的中点,点G、H分别在AA1、D1A1上,且满足AA1=3AG,D1H=2HA1,则异面直线EF、GH所成角的余弦值为$\frac{\sqrt{10}}{10}$.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,点E、F分别为边CC1、B1C1的中点,点G、H分别在AA1、D1A1上,且满足AA1=3AG,D1H=2HA1,则异面直线EF、GH所成角的余弦值为$\frac{\sqrt{10}}{10}$.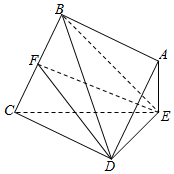 已知四棱锥E-ABCD的底面是边长为2的菱形,且AE⊥平面CDE,AE=1,CE=$\sqrt{7}$
已知四棱锥E-ABCD的底面是边长为2的菱形,且AE⊥平面CDE,AE=1,CE=$\sqrt{7}$