题目内容
5．求（1+2x-3x2）5展开式中x5的系数．分析 先化简所给的式子为：（1+2x-3x2）5=-（x-1）5（3x+1）5 ，再分别利用二项式定理的展开，展开式中x5的系数．
解答 解：∵（1+2x-3x2）5 =-（x-1）5（3x+1）5
=-（${C}_{5}^{0}$•x5-${C}_{5}^{1}$•x4+${C}_{5}^{2}$•x3-${C}_{5}^{3}$•x2+${C}_{5}^{4}$•x-${C}_{5}^{5}$）•[${C}_{5}^{0}$•（3x）5+${C}_{5}^{1}$•（3x）4+${C}_{5}^{2}$•（3x）3+${C}_{5}^{3}$•（3x）2+${C}_{5}^{4}$•（3x）+${C}_{5}^{5}$]
故（1+2x-3x2）5展开式里x5的系数为：-[${C}_{5}^{0}$•${C}_{5}^{5}$-${C}_{5}^{1}$•3${C}_{5}^{4}$+${C}_{5}^{2}$•9${C}_{5}^{3}$-${C}_{5}^{3}$•27${C}_{5}^{2}$+${C}_{5}^{4}$•81${C}_{5}^{1}$-${C}_{5}^{5}$•243${C}_{5}^{0}$]=92．
点评 本题主要考查二项式定理的应用，二项式展开式的通项公式，求展开式中某项的系数，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
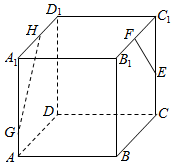如图所示，在棱长为2的正方体ABCD-A1B1C1D1中，点E、F分别为边CC1、B1C1的中点，点G、H分别在AA1、D1A1上，且满足AA1=3AG，D1H=2HA1，则异面直线EF、GH所成角的余弦值为$\frac{\sqrt{10}}{10}$．
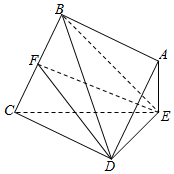已知四棱锥E-ABCD的底面是边长为2的菱形，且AE⊥平面CDE，AE=1，CE=$\sqrt{7}$