题目内容
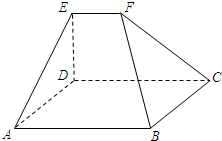如图，在五面体ABCDEF中，四边形ABCD是矩形，DE⊥平面ABCD．（1）求证：AB∥EF；
（2）求证：平面BCF⊥平面CDEF．
考点：平面与平面垂直的判定,空间中直线与直线之间的位置关系
专题：综合题,空间位置关系与距离
分析：（1）由四边形ABCD是矩形，得到AB∥平面CDEF，由此能证明AB∥EF．
（2）由已知条件推导出DE⊥BC，从而得到BC⊥平面CDEF，由此能证明平面BCF⊥平面CDEF．
（2）由已知条件推导出DE⊥BC，从而得到BC⊥平面CDEF，由此能证明平面BCF⊥平面CDEF．
解答：
证明：（1）因为四边形ABCD是矩形，所以AB∥CD，
因为AB?平面CDEF，CD?平面CDEF，
所以AB∥平面CDEF．…4分
因为AB?平面ABFE，平面ABFE∩平面CDEF=EF，
所以AB∥EF． …7分
（2）因为DE⊥平面ABCD，BC?平面ABCD，
所以DE⊥BC． …9分
因为BC⊥CD，CD∩DE=D，CD，DE?平面CDEF，
所以BC⊥平面CDEF． …12分
因为BC?平面BCF，所以平面BCF⊥平面CDEF．…14分．
因为AB?平面CDEF，CD?平面CDEF，
所以AB∥平面CDEF．…4分
因为AB?平面ABFE，平面ABFE∩平面CDEF=EF，
所以AB∥EF． …7分
（2）因为DE⊥平面ABCD，BC?平面ABCD，
所以DE⊥BC． …9分
因为BC⊥CD，CD∩DE=D，CD，DE?平面CDEF，
所以BC⊥平面CDEF． …12分
因为BC?平面BCF，所以平面BCF⊥平面CDEF．…14分．
点评：本题考查直线平行的证明，考查平面与平面垂直的证明，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
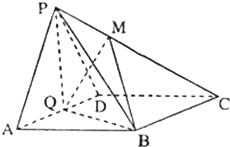如图，四棱锥P-ABCD中，四边形ABCD为平行四边形，面PAD⊥平面ABCD，PA=PD，Q为AD的中点，且QB⊥AD．
华罗庚中学高二排球队和篮球队各有10名同学，现测得排球队10人的身高（单位：cm）分别是：162、170、171、182、163、158、179、168、183、168，篮球队10人的身高（单位：cm）分别是：170、159、162、173、181、165、176、168、178、179．